题目内容
 折叠矩形的一边AD,点D落在BC边点F处,已知AB=8cm,BC=10cm,
折叠矩形的一边AD,点D落在BC边点F处,已知AB=8cm,BC=10cm,(1)说出图中哪些线段相等?
(2)写出全等的三角形;
(3)求EC的长.
分析:(1)根据翻折变换的性质和矩形的对边相等解答;
(2)根据翻折前后的两个三角形全等解答;
(3)在Rt△ABF中,利用勾股定理列式求出BF,然后求出FC,再用EC表示出EF,然后在Rt△CEF中,利用勾股定理列式计算即可得解.
(2)根据翻折前后的两个三角形全等解答;
(3)在Rt△ABF中,利用勾股定理列式求出BF,然后求出FC,再用EC表示出EF,然后在Rt△CEF中,利用勾股定理列式计算即可得解.
解答:解:(1)相等的线段有:AD=AF=BC,AB=CD,DE=EF;
(2)全等的三角形:△ADE≌△AFE;
(3)在Rt△ABF中,BF=
=
=6cm,
∴FC=BC-BF=10-6=4cm,
∵DE=EF,
∴EF=8-EC,
在Rt△CEF中,EC2+FC2=EF2,
即EC2+42=(8-EC)2,
解得EC=3cm.
(2)全等的三角形:△ADE≌△AFE;
(3)在Rt△ABF中,BF=
| AF2-AB2 |
| 102-82 |
∴FC=BC-BF=10-6=4cm,
∵DE=EF,
∴EF=8-EC,
在Rt△CEF中,EC2+FC2=EF2,
即EC2+42=(8-EC)2,
解得EC=3cm.
点评:本题考查了翻折变换的性质,矩形的对边相等的性质,勾股定理的应用,是基础题,熟记性质并准确识图是解题的关键.

练习册系列答案
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
 如图所示,矩形ABCD,折叠矩形的一边AD,使点D落在BC边的点F处,已知折痕AE=5
如图所示,矩形ABCD,折叠矩形的一边AD,使点D落在BC边的点F处,已知折痕AE=5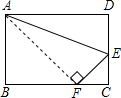 如右图,折叠矩形的一边AD,点D落在BC边上点F处,已知AB=8cm,BC=10cm,则EC的长是
如右图,折叠矩形的一边AD,点D落在BC边上点F处,已知AB=8cm,BC=10cm,则EC的长是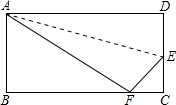 tan∠EFC=
tan∠EFC= cm,且tan∠EFC=
cm,且tan∠EFC= 。
。