题目内容
如图所示，矩形ABCD，折叠矩形的一边AD，使点D落在BC边的点F处，已知折痕AE=5| 5 |
| EC |
| FC |
| 3 |
| 4 |
（1）求证：△AFB∽△FEC；
（2）求矩形的周长．
分析：（1）矩形的特点是四个角均为直角，折叠的部分所包含的角也是直角，利用在直角三角形中两锐角互余可得∠BAF=∠CFE，进而可证明△ABF∽△FCE；
（2）利用相似三角形对应边成比例，再利用勾股定理即可得解．
（2）利用相似三角形对应边成比例，再利用勾股定理即可得解．
解答：证明：（1）∵四边形ABCD是矩形，
∴∠B=∠C=∠D=∠AFE=90°．
∵∠CFE+∠BFA=90°，∠BFA+∠BAF=90°，
∴∠BAF=∠CFE．
∴△ABF∽△FCE．
解：（2）∵
=
，设EC=3t，FC=4t，则EF=DE=5t，
∴AB=CD=8t．
∴
=
，
=
∴BF=6t．
∴AF=10t．
在Rt△AEF中，由勾股定理（10t）2+（5t）2=（5
）2
∴t=1．
∴矩形周长=2（AB+BF+FC）=2（8t+6t+4t）=36（cm）．
∴∠B=∠C=∠D=∠AFE=90°．
∵∠CFE+∠BFA=90°，∠BFA+∠BAF=90°，
∴∠BAF=∠CFE．
∴△ABF∽△FCE．
解：（2）∵
| EC |
| FC |
| 3 |
| 4 |
∴AB=CD=8t．
∴
| AB |
| FC |
| BF |
| CE |
| 8t |
| 4t |
| BF |
| 3t |
∴BF=6t．
∴AF=10t．
在Rt△AEF中，由勾股定理（10t）2+（5t）2=（5
| 5 |
∴t=1．
∴矩形周长=2（AB+BF+FC）=2（8t+6t+4t）=36（cm）．
点评：本题主要考查了矩形的特点、图形的折叠、相似三角形的判定定理及性质等内容．
练习册系列答案
相关题目
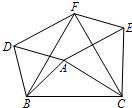18、如图所示，在△ABC中，分别以AB、AC、BC为边在BC的同侧作等边△ABD，等边△ACE、等边△BCF．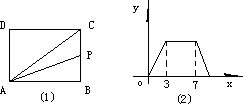
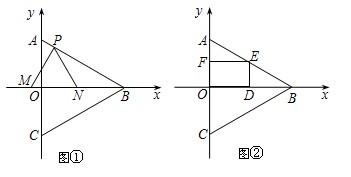
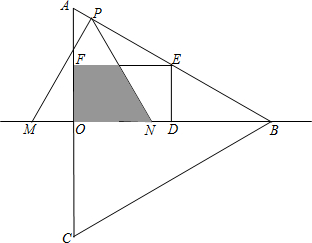边在△AOB内部作如图所示的矩形ODEF，点E在线段AB上．
（2012•邵阳）如图所示，在△ABC中，AB=AC，∠A＜90°，边BC、CA、AB的中点分别是D、E、F，则四边形AFDE是（ ）