题目内容
12.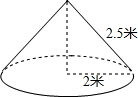 一把大遮阳伞,伞面撑开时可近似地看成是圆锥形,如图,它的母线长是2.5米,底面半径为2米,则做成这把遮阳伞需要布料的面积是( )平方米(接缝不计).
一把大遮阳伞,伞面撑开时可近似地看成是圆锥形,如图,它的母线长是2.5米,底面半径为2米,则做成这把遮阳伞需要布料的面积是( )平方米(接缝不计).| A. | $\frac{25}{4}$π | B. | 5π | C. | 4π | D. | 3π |
分析 根据圆锥的侧面展开图是扇形可知,求得圆锥的底面周长就是圆锥的弧长,利用圆锥的面积计算方法求得圆锥的侧面积即可.
解答 解:圆锥的底面周长=2πr=2π×2=4π,
∵圆锥的底面周长等于圆锥的侧面展开扇形的弧长,
∴圆锥的侧面积=$\frac{1}{2}$lr=$\frac{1}{2}$×4π×2.5=5π,
故选B.
点评 本题考查了圆锥的侧面积的计算,解题的关键是正确的理解圆锥的底面周长等于圆锥的侧面展开扇形的面积.

练习册系列答案
相关题目
1.若函数y=(m-2)x的图象经过第二、四象限,则m的取值范围是( )
| A. | m>2 | B. | m<2 | C. | m≥2 | D. | m≤2 |
20.如果关于x的一元二次方程x2+px+q=0的两根分别为x1=-3,x2=2,那么p、q的值分别是( )
| A. | 1,-6 | B. | -1,-6 | C. | -1,6 | D. | 1,6 |
7.已知x2-x-1=0,则x3-2x+1的值为( )
| A. | $\sqrt{5}$-1 | B. | 2 | C. | -1 | D. | -2 |
17.若3a=4b,则$\frac{a}{b}$=( )
| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{2}$ | D. | $\frac{2}{3}$ |
2. 用两块相同的三角板按如图所示的方式作平行线AB和CD,能解释其中的道理的依据是( )
用两块相同的三角板按如图所示的方式作平行线AB和CD,能解释其中的道理的依据是( )
 用两块相同的三角板按如图所示的方式作平行线AB和CD,能解释其中的道理的依据是( )
用两块相同的三角板按如图所示的方式作平行线AB和CD,能解释其中的道理的依据是( )| A. | 内错角相等,两直线平行 | B. | 同位角相等,两直线平行 | ||
| C. | 同旁内角互补,两直线平行 | D. | 平行于同一直线的两直线平行 |
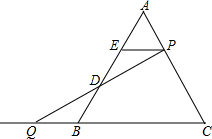 如图,△ABC是等边三角形,P是AC边上任意一点(与A、C两点不重合),Q是CB延长线上一点,且始终满足条件BQ=AP,过P作PE∥BC交AB于点E,连接PQ交AB于D.
如图,△ABC是等边三角形,P是AC边上任意一点(与A、C两点不重合),Q是CB延长线上一点,且始终满足条件BQ=AP,过P作PE∥BC交AB于点E,连接PQ交AB于D.