题目内容
矩形的周长是8+8 ,两对角线夹角为60°,则矩形的面积是________.
,两对角线夹角为60°,则矩形的面积是________.
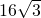
分析:根据矩形对角线相等且互相平分,对角线夹角为60°可以证明△ADO为等边三角形,根据勾股定理即可证明AB=
 AD,根据周长求得AD的长,根据AD,AB计算矩形ABCD的面积.
AD,根据周长求得AD的长,根据AD,AB计算矩形ABCD的面积.解答:
 解:矩形对角线相等且互相平分,∴AO=DO,
解:矩形对角线相等且互相平分,∴AO=DO,∵∠AOD=60°,∴△ADO为等边三角形,
即AD=AO=DO,
∴AB=
 AD,
AD,即(2
 +2)AD=8
+2)AD=8 +8,
+8,AD=4,
∴矩形ABCD的面积为16
 .
.故答案为 16
 .
.点评:本题考查了矩形对角线相等且互相平分的性质,考查了勾股定理在直角三角形中的运用,本题中求AD的长是解题的关键.

练习册系列答案
相关题目
矩形的一条长边的中点与另一条长边构成等腰直角三角形,已知矩形的周长是36,则矩形一条对角线长是( )
A、6
| ||
B、5
| ||
C、4
| ||
D、3
|
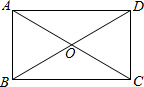 如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86厘米,矩形的周长是30厘米,则对角线的长是
如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86厘米,矩形的周长是30厘米,则对角线的长是