题目内容
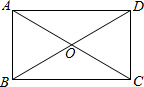 如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86厘米,矩形的周长是30厘米,则对角线的长是
如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86厘米,矩形的周长是30厘米,则对角线的长是14
14
厘米.分析:根据矩形性质得出OA=OB=OC=OD,AB=CD,AD=BC,求出8OA+2AB+2BC=86厘米和2AB+2BC=30厘米,求出OA,即可求出答案.
解答:解:∵四边形ABCD是矩形,
∴AB=CD,AD=BC,AC=BF,AO=OC,OD=OB,
∴AO=OC=OD=OB,
∵矩形ABCD被两条对角线分成四个小三角形的周长的和是86厘米,
∴OA+OD+AD+OD+OC+CD+OC+OB+BC+OA+OB+AB=86厘米,
即8OA+2AB+2BC=86厘米,
∵矩形ABCD的周长是30厘米,
∴2AB+2BC=30厘米,
∴8OA=56厘米,
∴OA=7厘米,
即AC=BD=2OA=14厘米.
故答案为:14.
∴AB=CD,AD=BC,AC=BF,AO=OC,OD=OB,
∴AO=OC=OD=OB,
∵矩形ABCD被两条对角线分成四个小三角形的周长的和是86厘米,
∴OA+OD+AD+OD+OC+CD+OC+OB+BC+OA+OB+AB=86厘米,
即8OA+2AB+2BC=86厘米,
∵矩形ABCD的周长是30厘米,
∴2AB+2BC=30厘米,
∴8OA=56厘米,
∴OA=7厘米,
即AC=BD=2OA=14厘米.
故答案为:14.
点评:本题考查了矩形的性质的应用,注意:矩形的对边相等,矩形的对角线互相平分且相等.

练习册系列答案
相关题目
 9、如图,矩形ABCD被分割成六个正方形,其中最小正方形的面积等于1,则矩形ABCD的面积等于( )
9、如图,矩形ABCD被分割成六个正方形,其中最小正方形的面积等于1,则矩形ABCD的面积等于( )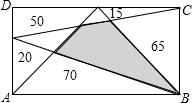 如图,矩形ABCD被分成8块,图中的数字是其中5块的面积数,则图中阴影部分的面积为
如图,矩形ABCD被分成8块,图中的数字是其中5块的面积数,则图中阴影部分的面积为
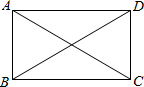 如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86cm,对角线长是13cm,那么矩形的周长是多少?
如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86cm,对角线长是13cm,那么矩形的周长是多少?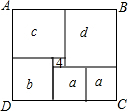 如图,矩形ABCD被分成六个大小不一的正方形,已知中间一个小正方形面积为4,其他正方形的边长分别为a、b、c、d.求矩形ABCD中最大正方形与最小正方形的面积之差.
如图,矩形ABCD被分成六个大小不一的正方形,已知中间一个小正方形面积为4,其他正方形的边长分别为a、b、c、d.求矩形ABCD中最大正方形与最小正方形的面积之差.