题目内容
 如图,平面直角坐标系中,矩形OABC的对角线AC=10,边OA=6.
如图,平面直角坐标系中,矩形OABC的对角线AC=10,边OA=6.(1)求C点的坐标;
(2)把矩形OABC沿直线DE对折使点C落在点A处,直线DE与OC、AC、AB的交点分别为D,F,E,求折痕DE的长;
(3)若点M在x轴上,平面内是否存在点N,使以M、D、F、N为顶点的四边形是菱形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
考点:一次函数综合题,全等三角形的判定与性质,勾股定理,菱形的性质,相似三角形的判定与性质
专题:
分析:(1)要求点C的坐标,只需运用勾股定理求出OC即可.
(2)易证△AFE≌△CFD,得到EF=DF,要求DE,只需求出DF.先证明△DFC∽△AOC,再根据相似三角形的对应边成比例就可求出DF,进而求出DE.
(3)构成菱形的四个顶点的顺序不定,需分情况讨论.由于D、F是定点,可将线段DF分为两大类:DF为菱形的一边、DF为菱形的对角线.然后分别讨论即可.
(2)易证△AFE≌△CFD,得到EF=DF,要求DE,只需求出DF.先证明△DFC∽△AOC,再根据相似三角形的对应边成比例就可求出DF,进而求出DE.
(3)构成菱形的四个顶点的顺序不定,需分情况讨论.由于D、F是定点,可将线段DF分为两大类:DF为菱形的一边、DF为菱形的对角线.然后分别讨论即可.
解答:解: (1)∵四边形OABC是矩形,
(1)∵四边形OABC是矩形,
∴∠AOC=90°.
∵AC=10,OA=6,
∴OC=8.
∴C点的坐标为(8,0).
(2)由折叠可得:DE⊥AC,AF=FC=5.
∵∠FCD=∠OCA,∠DFC=∠AOC=90°,
∴△DFC∽△AOC.
∴
=
=
.
∴
=
=
.
∴DF=
,DC=
.
∴OD=OC-DC=8-
=
.
∵四边形OABC是矩形,
∴AB∥DC,
∴∠EAF=∠DCF
在△AFE和△CFD中,
.
∴△AFE≌△CFD(ASA).
∴EF=DF.
∴DE=2DF=2×
=
.
∴折痕DE的长为
.
(3)过点F作FH⊥DC,垂足为H,如图2,
∵S△DFC=
DF•FC=
DC•FH,DF=
,FC=5,DC=
,
∴FH=3.
∵FH⊥DC,DF=
,FH=3,
∴DH=
.
∴OH=OD+DH=4.
∴F(4,3).
①若DF为菱形的一边
当DM为菱形的对角线时,如图3.点N与点F关于x轴对称,则点N的坐标为(4,-3).
当DM为菱形的另一边时,如图4. 此时FN∥DM,FN=DF=
此时FN∥DM,FN=DF=
.
∵F(4,3),
∴点N的坐标为(4-
,3)或(4+
,3)即(
,3)或(
,3).
②若DF为菱形的对角线,如图5.
∵四边形DNFM为菱形,
∴MN⊥DF,DG=
DF.
∵DF⊥AC,
∴∠DGM=∠DFC=90°.
∴MN∥AC.
∴△DGM∽△DFC.
∴
=
=
.
∴DM=
DC=
.
∵四边形DNFM为菱形,
∴NF∥DM,NF=DM=
.
∴点N的坐标为(4-
,3)即(
,3).
综上所述:符合要求的点N的坐标可能为(4,-3)、(
,3)、(
,3)、(
,3).
 (1)∵四边形OABC是矩形,
(1)∵四边形OABC是矩形,∴∠AOC=90°.
∵AC=10,OA=6,
∴OC=8.
∴C点的坐标为(8,0).
(2)由折叠可得:DE⊥AC,AF=FC=5.
∵∠FCD=∠OCA,∠DFC=∠AOC=90°,
∴△DFC∽△AOC.
∴
| DF |
| AO |
| FC |
| OC |
| DC |
| AC |
∴
| DF |
| 6 |
| 5 |
| 8 |
| DC |
| 10 |
∴DF=
| 15 |
| 4 |
| 25 |
| 4 |
∴OD=OC-DC=8-
| 25 |
| 4 |
| 7 |
| 4 |
∵四边形OABC是矩形,
∴AB∥DC,
∴∠EAF=∠DCF
在△AFE和△CFD中,
|
∴△AFE≌△CFD(ASA).

∴EF=DF.
∴DE=2DF=2×
| 15 |
| 4 |
| 15 |
| 2 |
∴折痕DE的长为
| 15 |
| 2 |
(3)过点F作FH⊥DC,垂足为H,如图2,
∵S△DFC=
| 1 |
| 2 |
| 1 |
| 2 |
| 15 |
| 4 |
| 25 |
| 4 |
∴FH=3.
∵FH⊥DC,DF=
| 15 |
| 4 |
∴DH=
| 9 |
| 4 |
∴OH=OD+DH=4.
∴F(4,3).
①若DF为菱形的一边
当DM为菱形的对角线时,如图3.点N与点F关于x轴对称,则点N的坐标为(4,-3).
当DM为菱形的另一边时,如图4.
 此时FN∥DM,FN=DF=
此时FN∥DM,FN=DF=| 15 |
| 4 |
∵F(4,3),
∴点N的坐标为(4-
| 15 |
| 4 |
| 15 |
| 4 |
| 1 |
| 4 |
| 31 |
| 4 |
②若DF为菱形的对角线,如图5.
∵四边形DNFM为菱形,
∴MN⊥DF,DG=
| 1 |
| 2 |
∵DF⊥AC,
∴∠DGM=∠DFC=90°.
∴MN∥AC.
∴△DGM∽△DFC.
∴
| DM |
| DC |
| DG |
| DF |
| 1 |
| 2 |
∴DM=
| 1 |
| 2 |
| 25 |
| 8 |
∵四边形DNFM为菱形,
∴NF∥DM,NF=DM=
| 25 |
| 8 |
∴点N的坐标为(4-
| 25 |
| 8 |
| 7 |
| 8 |
综上所述:符合要求的点N的坐标可能为(4,-3)、(
| 1 |
| 4 |
| 31 |
| 4 |
| 7 |
| 8 |
点评:本题运用了矩形的性质、菱形的性质、三角形相似(包括全等)的性质及判定、勾股定理等知识,综合性强;另外,还考查了分类讨论的思想,注重对学生知识和能力的考查,是一条好题.

练习册系列答案
相关题目
 如图,两个高度相等的圆柱形水杯,甲杯装满液体,乙杯是空杯,若把甲杯中的液体全部倒入乙杯,则图中点P与液面的距离是
如图,两个高度相等的圆柱形水杯,甲杯装满液体,乙杯是空杯,若把甲杯中的液体全部倒入乙杯,则图中点P与液面的距离是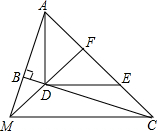 如图,∠ABC=90°,D、E分别在BC、AC上,AD⊥DE,且AD=DE,点F是AE的中点,FD与AB相交于点M.
如图,∠ABC=90°,D、E分别在BC、AC上,AD⊥DE,且AD=DE,点F是AE的中点,FD与AB相交于点M.
 为了维护海洋权益,新组建的国家海洋局加强了海洋巡逻力度.如图,一艘海监船位于灯塔P南偏东45°方向,距离灯塔100海里的A处,沿正北方向航行一段时间后,到达位于灯塔P北偏东30°方向上的B处.
为了维护海洋权益,新组建的国家海洋局加强了海洋巡逻力度.如图,一艘海监船位于灯塔P南偏东45°方向,距离灯塔100海里的A处,沿正北方向航行一段时间后,到达位于灯塔P北偏东30°方向上的B处. 如图,直线y=-x+3与x轴交于点C,与y轴交于点A,点B的坐标为(2,3)抛物线y=-x2+bx+c经过A、C两点.
如图,直线y=-x+3与x轴交于点C,与y轴交于点A,点B的坐标为(2,3)抛物线y=-x2+bx+c经过A、C两点.
 已知某市2013年企业用水量x(吨)与该月应交的水费y(元)之间的函数关系如图所示.
已知某市2013年企业用水量x(吨)与该月应交的水费y(元)之间的函数关系如图所示. 如图,A、B、C是⊙O上的三点,∠AOB=100°,则∠ACB=
如图,A、B、C是⊙O上的三点,∠AOB=100°,则∠ACB=