Question

（2012•丰泽区质检）如图，已知抛物线y=-

1

4

x2+bx+4经过点（-2，0），与y轴交于A点，与x轴交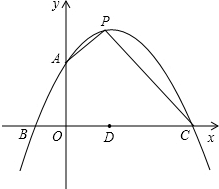于B、C两点．
（1）求b的值；
（2）设以线段BC为直径的圆的圆心为点D，试判断点A与⊙D的位置关系，并说明理由；
（3）设P是抛物线上一个动点，且点P位于第一象限内，求当四边形PAOC的面积最大时，求点P的坐标．

Answer 1

分析：（1）根据抛物线经过点（-2，0），代入即可得出b的值；
（2）先求出点D、点A的坐标，然后求出DA的长，将DA的长与⊙D的半径进行比较即可．
（3）设出点P坐标，然后可得S_PAOC=S_△PAO+S_△POC，从而得出关于x的二次函数，利用配方法求最值即可，从而可得出点P的坐标．

解答：解：（1）∵抛物线y=-

1

4

x2+bx+4经过点（-2，0），
∴-

1

4

×（-2）²+b×（-2）+4=0，
解得：b=

3

2

．
（2）令-

1

4

x2+

3

2

x+4=0，
解得：x₁=-2，x₂=8，
故点B（-2，0），C（8，0），也可得出BC=10，D（3，0），
即⊙D的半径R=5，
令x=0得：y=4，即OA=4，
∵AD=

OA2+OD2

=

42+32

=5=R，
∴点AD 在⊙D上．
（3）连接OP，设P（x，-

1

4

x²+

3

2

x+4），

则四边形PAOC的面积为：S_PAOC=S_△PAO+S_△POC=

1

2

OA×x+

1

2

OC×（-

1

4

x²+

3

2

x+4）
=2x+4（-

1

4

x²+

3

2

x+4）
=-x²+8x+16
=-（x+4）²+32，
故当x=4，即P的坐标为（4，6）时，S_{四边形PAOC}最大．

点评：此题考查了二次函数综合题，涉及了待定系数法求函数解析式、点与圆的位置关系及二次函数的最值，难点在第三问，要注意将不规则图形分成两个三角形，从而转化后利用函数的最值计算，难度较大．