题目内容
 如图,直线y=-
如图,直线y=-| 1 |
| 2 |
| k |
| x |
| 8 |
| 5 |
| 8 |
| 5 |
分析:过B作x轴、y轴的垂线,垂足分别为E、F,令直线方程中x=0,求出y的值,即为点A的纵坐标,得出OA的长,令y=0求出x的值,即为D的横坐标,确定出OD的长,由FB与OD平行,利用平行线得比例列出比例式,根据OA:OD的比值,得出AF:FB的比值,设B的坐标为(m,n),可得出FB=m,根据比例表示出AF的长,在直角三角形AFB中,利用勾股定理表示出AB的平方,由OD-OE=ED,表示出ED,BE即为B的纵坐标n,在直角三角形BED中,根据勾股定理表示出BD的平方,再把B的坐标代入直线方程,表示出2b-m=2n,即为DE的长,代入BD的平方,整理后开方求出AB•BD的值,代入已知AB•BD=4中,求出mn的值,又B在反比例函数图象上,可得出k=mn,由mn的值可得出k的值.
解答:解:过B分别作x轴和y轴的垂线,E,F分别为垂足,如图,

对于y=-
x+b,令x=0,y=b;令y=0,x=2b,
∴A(0,b),D(2b,0),即OA=b,OD=2b,
∵BF∥OD,
∴AF:OA=BF:OD,又OA:OD=1:2,
∴AF:BF=1:2,
设B(m,n),m>0,n>0,则AF=
m,BF=m,
∴在Rt△AFB中,根据勾股定理得:AB2=AF2+BF2=
m2,
在Rt△BED中,BE=n,DE=OD-OE=OD-FB=2b-m,
根据勾股定理得:BD2=BE2+DE2=n2+(2b-m)2,
而B点在直线y=-
x+b上,
∴n=-
m+b,即2b-m=2n,
∴BD2=n2+4n2=5n2,
又AB•BD=4,且m>0,n>0,
∴
m2•5n2=16,即m•n=
,
∵点B在双曲线y=
的图象上,
∴k=m•n=
.
故答案为:

对于y=-
| 1 |
| 2 |
∴A(0,b),D(2b,0),即OA=b,OD=2b,
∵BF∥OD,
∴AF:OA=BF:OD,又OA:OD=1:2,
∴AF:BF=1:2,
设B(m,n),m>0,n>0,则AF=
| 1 |
| 2 |
∴在Rt△AFB中,根据勾股定理得:AB2=AF2+BF2=
| 5 |
| 4 |
在Rt△BED中,BE=n,DE=OD-OE=OD-FB=2b-m,
根据勾股定理得:BD2=BE2+DE2=n2+(2b-m)2,
而B点在直线y=-
| 1 |
| 2 |
∴n=-
| 1 |
| 2 |
∴BD2=n2+4n2=5n2,
又AB•BD=4,且m>0,n>0,
∴
| 5 |
| 4 |
| 8 |
| 5 |
∵点B在双曲线y=
| k |
| x |
∴k=m•n=
| 8 |
| 5 |
故答案为:
| 8 |
| 5 |
点评:此题属于反比例函数的综合题,涉及的知识有:平行线的性质,勾股定理,代数式的变形,线段长度与坐标的关系,以及一次函数与坐标轴的交点,其中作出辅助线BE、BF是本题的突破点.

练习册系列答案
 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
 如图,直线EF过平行四边形ABCD对角线的交点O,分别交AB、CD于E、F,若平行四边形的面积是12,则△AOE与△DOF的面积和为( )
如图,直线EF过平行四边形ABCD对角线的交点O,分别交AB、CD于E、F,若平行四边形的面积是12,则△AOE与△DOF的面积和为( )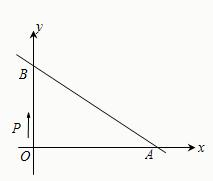 点出发,沿路线O→B→A以每秒1个单位长度的速度运动,到达A点时运动停止.
点出发,沿路线O→B→A以每秒1个单位长度的速度运动,到达A点时运动停止. 如图,直线
如图,直线 如图,直线
如图,直线