题目内容
7.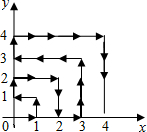 如图,一个粒子在第一象限内及x轴,y轴上运动,第一分钟内从原点运动到(1,0),第二分钟从(1,0)运动到(1,1),而后它接着按图中箭头所示的与x轴,y轴平行的方向来回运动,且每分钟移动1个长度单位.
如图,一个粒子在第一象限内及x轴,y轴上运动,第一分钟内从原点运动到(1,0),第二分钟从(1,0)运动到(1,1),而后它接着按图中箭头所示的与x轴,y轴平行的方向来回运动,且每分钟移动1个长度单位.(1)当粒子所在位置是(2,2)时,所经过的时间是6分钟;
(2)在第2014分钟时,这个粒子所在位置的坐标是(44,10).
分析 (1)根据粒子的运动规律可知:从原点到(0,1)粒子运动了3个单位长度,用了3分钟,从(0,2)到(2,0)粒子运动了5个单位长度,用了5分钟,依此类推,可确定从(0,n)到(n,0)粒子终点在x轴上时的偶数n时的总时间及从(n,0)到(0,n)粒子终点在y轴上时的奇数n时总时间;
(2)由(1),当到(44,44)处,粒子运动了44×45=1980分钟,方向向下,到2004分钟,由(44,44)再向下运动2014-1980=34分钟,即可推得2014分钟这个粒子所处的位置.
解答 解:(1)粒子所在位置与运动的时间的情况如下:
位置:(1,1)运动了2=1×2分钟,方向向左,
位置:(2,2)运动了6=2×3分钟,方向向下,
(2)到(44,44)处,粒子运动了44×45=1980分钟,方向向下,
故到2014分钟,须由(44,44)再向下运动2014-1980=34分钟,
到达(44,10).
故答案为:(1)6分钟;(2)(44,10).
点评 本题是考查了点的坐标的确定.本题也是一个阅读理解并猜想规律的题目,解答此题的关键是总结规律首先确定点所在的大致位置,然后就可以进一步推得点的坐标.

练习册系列答案
相关题目
16.当x取任意实数时,下列各根式有意义的是( )
| A. | $\sqrt{x+1}$ | B. | $\sqrt{\frac{x-1}{2}}$ | C. | $\sqrt{\frac{3}{{x}^{2}}}$ | D. | $\sqrt{|x|+1}$ |
17.如果点P(a,b)在x轴上,那么点Q(ab,-1)在( )
| A. | y轴的正半轴上 | B. | y轴的负半轴上 | C. | x轴的正半轴上 | D. | x轴的负半轴上 |
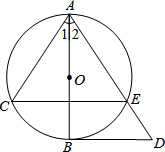 如图,AB为⊙O的直径,劣弧$\widehat{BC}$=$\widehat{BE}$,BD∥CE,连接AE并延长交BD于D.求证:
如图,AB为⊙O的直径,劣弧$\widehat{BC}$=$\widehat{BE}$,BD∥CE,连接AE并延长交BD于D.求证: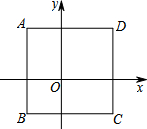 如图,正方形ABCD在平面直角坐标系中,其中三个顶点的坐标分别为A(-2,3),B(-2,-2),C(3,-2),则第四个顶点D的坐标为(3,3).
如图,正方形ABCD在平面直角坐标系中,其中三个顶点的坐标分别为A(-2,3),B(-2,-2),C(3,-2),则第四个顶点D的坐标为(3,3).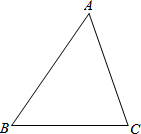 按要求在图中画图,并把答案填写在横线上.
按要求在图中画图,并把答案填写在横线上.
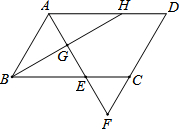 如图,?ABCD中,∠DAB的平分线交BC于E,交DC的延长线于F,∠ABC的平分线交AD于点H,交AF于点G.
如图,?ABCD中,∠DAB的平分线交BC于E,交DC的延长线于F,∠ABC的平分线交AD于点H,交AF于点G.