Question

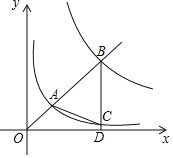
【题目】如图，在等边△ABC中，AB=4，D是BC的中点，将△ABD绕点A旋转后得到△ACE，连接DE交AC于点F，则△AEF的面积为_______．

Answer 1

【答案】

【解析】

首先，利用等边三角形的性质求得AD=2；然后根据旋转的性质、等边三角形的性质推知△ADE为等边三角形，则DE=AD，便可求出EF和AF，从而得到△AEF的面积.

解：∵在等边△ABC中，∠B=60，AB=4，D是BC的中点，

∴AD⊥BC，∠BAD=∠CAD=30，

∴AD=ABcos30=4×=2，

根据旋转的性质知，∠EAC=∠DAB=30，AD=AE，

∴∠DAE=∠EAC+∠CAD=60，

∴△ADE的等边三角形，

∴DE=AD=2，∠AEF=60,

∵∠EAC=∠CAD

∴EF=DF=，AF⊥DE

∴AF=EFtan60=×=3，

∴S△AEF=EF×AF=××3=.

故答案为：.