题目内容
如图,在梯形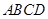 中,
中, 为
为 的中点,
的中点, 交
交 于点
于点 .
.
(1)求证: ;
;
(2)当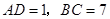 ,且
,且 平分
平分 时,求
时,求 的长.
的长.

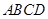 中,
中, 为
为 的中点,
的中点, 交
交 于点
于点 .
.(1)求证:
 ;
;(2)当
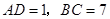 ,且
,且 平分
平分 时,求
时,求 的长.
的长.
(1)证明详见解析.(2)EF=4.
试题分析:根据题意构造辅助线,利用中线性质和平行四边形性质即可得出结论.
(1)过D作DM∥AB,∵AD∥BC,DM∥AB,∴四边形ABMD为平行四边形,∴BM=AD∵
 ,∴EF∥DM,又∵E为CD的中点∴F为CM中点即MF=CF,∴BF=BM+MF=AD+CF.
,∴EF∥DM,又∵E为CD的中点∴F为CM中点即MF=CF,∴BF=BM+MF=AD+CF.(2)过E作EH⊥AB,∵BE平分
 ,∴CE=EH=DE(角平分线上一点到角两边的距离相等),在Rt△ADE和Rt△AHE中,DE=EH,AE=AE∴Rt△ADE≌Rt△AHE(SH定理)∴AH=AD=1,同理可得BH=BC=7,∴AB=AH+BH=8∵四边形ABMD为平行四边形,∴DM=AB=8,又∵E、F分别为CD、CM中点,∴
,∴CE=EH=DE(角平分线上一点到角两边的距离相等),在Rt△ADE和Rt△AHE中,DE=EH,AE=AE∴Rt△ADE≌Rt△AHE(SH定理)∴AH=AD=1,同理可得BH=BC=7,∴AB=AH+BH=8∵四边形ABMD为平行四边形,∴DM=AB=8,又∵E、F分别为CD、CM中点,∴ .
.
练习册系列答案
相关题目



 和
和 的角平分线AE、AF上,BD交AC于点O,如果O是BD的中点,试找出当点O在AC的什么位置时,四边形ABCD是矩形,并说明理由.
的角平分线AE、AF上,BD交AC于点O,如果O是BD的中点,试找出当点O在AC的什么位置时,四边形ABCD是矩形,并说明理由.

