题目内容
 如图,点D在BC上,DE⊥AB于点E,DF⊥BC交AC于点F,BD=CF,BE=CD.若∠AFD=145°,则∠EDF=
如图,点D在BC上,DE⊥AB于点E,DF⊥BC交AC于点F,BD=CF,BE=CD.若∠AFD=145°,则∠EDF=考点:全等三角形的判定与性质
专题:
分析:由图示知:∠FDC+∠AFD=180°,则∠FDC=35°.通过全等三角形Rt△BDE≌△Rt△CFD(HL)的对应角相等推知∠BDE=∠CFD.
解答:解:如图,∵∠FDC+∠AFD=145°,∠AFD=145°,
∴∠FDC=35°.
又∵DE⊥AB,DF⊥BC,
∴∠BED=∠CDF=90°,
在Rt△BDE与△Rt△CFD中,
,
∴Rt△BDE≌△Rt△CFD(HL),
∴∠BDE=∠CFD=35°,
∴∠EDF+∠BDE=∠EDF+∠CFD=90°,
∴∠EDF=55°.
故答案是:55°.
∴∠FDC=35°.
又∵DE⊥AB,DF⊥BC,
∴∠BED=∠CDF=90°,
在Rt△BDE与△Rt△CFD中,
|
∴Rt△BDE≌△Rt△CFD(HL),
∴∠BDE=∠CFD=35°,
∴∠EDF+∠BDE=∠EDF+∠CFD=90°,
∴∠EDF=55°.
故答案是:55°.
点评:本题考查了全等三角形的判定与性质.全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.

练习册系列答案
相关题目
 如图,点B是△ADC的边AD的延长线上一点,DE∥AC.若∠C=50°,∠A=60°,则∠ADE的度数等于( )
如图,点B是△ADC的边AD的延长线上一点,DE∥AC.若∠C=50°,∠A=60°,则∠ADE的度数等于( )| A、130° | B、120° |
| C、110° | D、70° |
已知x+y=3,x-y=1,则下列计算不正确的是( )
| A、(x+y)2=9 |
| B、x2+y2=5 |
| C、xy=8 |
| D、x2-y2=3 |
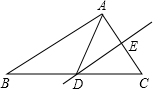 如图,△ABC中,DE是AC的中垂线,AE=7cm,△ABC的周长为35cm,则△ABD的周长是
如图,△ABC中,DE是AC的中垂线,AE=7cm,△ABC的周长为35cm,则△ABD的周长是 如图,A、D是⊙O上的两个点,BC是直径,若∠D=35°,则∠COA的度数是
如图,A、D是⊙O上的两个点,BC是直径,若∠D=35°,则∠COA的度数是