题目内容
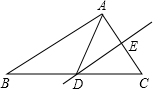如图，△ABC中，DE是AC的中垂线，AE=7cm，△ABC的周长为35cm，则△ABD的周长是考点：线段垂直平分线的性质
专题：
分析：根据线段垂直平分线的性质可得AD=CD，AE=CE，再根据△ABC的周长为35cm，可得AB+BD+CD+AC=35cm，进而得到AB+BD+DC=AB+AD+DB=35-14=21cm．
解答：解：∵DE是AC的中垂线，
∴AD=CD，AE=CE，
∵△ABC的周长为35cm，
∴AB+BD+CD+AC=35cm，
∵AE=7cm，
∴AC=14cm，
∴AB+BD+DC=AB+AD+DB=35-14=21cm，
故答案为：21cm．
∴AD=CD，AE=CE，
∵△ABC的周长为35cm，
∴AB+BD+CD+AC=35cm，
∵AE=7cm，
∴AC=14cm，
∴AB+BD+DC=AB+AD+DB=35-14=21cm，
故答案为：21cm．
点评：此题主要考查了线段垂直平分线的性质，关键是掌握垂直平分线上任意一点，到线段两端点的距离相等．
练习册系列答案
阅读快车系列答案
相关题目
如图，四边形ABCD是正方形，E是CD边上一点，连接AE，延长CB至点F，使得BF=DE，连接AF，则AF=
如图，点D在BC上，DE⊥AB于点E，DF⊥BC交AC于点F，BD=CF，BE=CD．若∠AFD=145°，则∠EDF=
若一个长方体从左面、上面看到的形状图及相关的数据如图，则从正面看到的形状图的面积为
如图，点C、F在线段BE上，且∠1=∠2，AC=DF，下列条件不能使△ABC≌△DEF的为（ ）| A、∠B=∠E |
| B、∠A=∠D |
| C、BF=CE |
| D、AB=DE |
已知-6a8b4和是5a4nb4同类项，则代数式12n-10的值是（ ）
| A、12 | B、13 | C、14 | D、15 |