题目内容
如图,AB∥CD,分别探讨下面四个图形中∠APC与∠PAB、∠PCD的关系,请你从所得到的关系中任选一个加以说明。(适当添加辅助线,其实并不难)
见解析
解析

练习册系列答案
相关题目
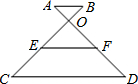 如图,AB∥CD,BO:OC=1:4,点E、F分别是OC、OD的中点,则EF:AB的值为( )
如图,AB∥CD,BO:OC=1:4,点E、F分别是OC、OD的中点,则EF:AB的值为( )| A、1 | B、2 | C、3 | D、4 |
题目内容
如图,AB∥CD,分别探讨下面四个图形中∠APC与∠PAB、∠PCD的关系,请你从所得到的关系中任选一个加以说明。(适当添加辅助线,其实并不难)
见解析
解析

 如图,AB∥CD,BO:OC=1:4,点E、F分别是OC、OD的中点,则EF:AB的值为( )
如图,AB∥CD,BO:OC=1:4,点E、F分别是OC、OD的中点,则EF:AB的值为( )| A、1 | B、2 | C、3 | D、4 |