题目内容
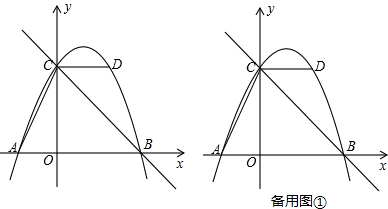
13. 如图,在Rt△ABC中,∠ACB=90°,AC=2$\sqrt{3}$,以点C为圆心,CB的长为半径画弧,与AB边交于点D,将$\widehat{BD}$绕点D旋转180°后点B与点A恰好重合,则图中阴影部分的面积为$2\sqrt{3}-\frac{2π}{3}$.
如图,在Rt△ABC中,∠ACB=90°,AC=2$\sqrt{3}$,以点C为圆心,CB的长为半径画弧,与AB边交于点D,将$\widehat{BD}$绕点D旋转180°后点B与点A恰好重合,则图中阴影部分的面积为$2\sqrt{3}-\frac{2π}{3}$.
分析 阴影部分的面积=三角形的面积-扇形的面积,根据面积公式计算即可.
解答 解:由旋转可知AD=BD,
∵∠ACB=90°,AC=2$\sqrt{3}$,
∴CD=BD,
∵CB=CD,
∴△BCD是等边三角形,
∴∠BCD=∠CBD=60°,
∴BC=$\frac{\sqrt{3}}{3}$AC=2,
∴阴影部分的面积=2$\sqrt{3}$×2÷2-$\frac{60π×{2}^{2}}{360}$=$2\sqrt{3}-\frac{2π}{3}$.
故答案为:$2\sqrt{3}-\frac{2π}{3}$.
点评 本题考查了三角形和扇形的面积公式及三角函数值,关键是得到△BCD是等边三角形.

练习册系列答案
相关题目
1. 如图是一个正方体的平面展开图,把展开图折叠成正方体后,“美”字一面相对面的字是( )
如图是一个正方体的平面展开图,把展开图折叠成正方体后,“美”字一面相对面的字是( )
 如图是一个正方体的平面展开图,把展开图折叠成正方体后,“美”字一面相对面的字是( )
如图是一个正方体的平面展开图,把展开图折叠成正方体后,“美”字一面相对面的字是( )| A. | 丽 | B. | 连 | C. | 云 | D. | 港 |
18.若一个正n边形的每个内角为144°,则这个正n边形的所有对角线的条数是( )
| A. | 7 | B. | 10 | C. | 35 | D. | 70 |
5.-2的相反数是( )
| A. | $\frac{1}{2}$ | B. | ±2 | C. | 2 | D. | -$\frac{1}{2}$ |
11. 如图,将正六边形ABCDEF放置在直角坐标系内,A(-2,0),点B在原点,把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转,每次翻转60°,经过2016次翻转之后,点C的坐标是( )
如图,将正六边形ABCDEF放置在直角坐标系内,A(-2,0),点B在原点,把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转,每次翻转60°,经过2016次翻转之后,点C的坐标是( )
 如图,将正六边形ABCDEF放置在直角坐标系内,A(-2,0),点B在原点,把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转,每次翻转60°,经过2016次翻转之后,点C的坐标是( )
如图,将正六边形ABCDEF放置在直角坐标系内,A(-2,0),点B在原点,把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转,每次翻转60°,经过2016次翻转之后,点C的坐标是( )| A. | (4032,0) | B. | (4032,2$\sqrt{3}$) | C. | (4031,$\sqrt{3}$) | D. | (4033,$\sqrt{3}$) |
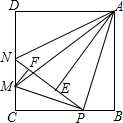 如图,在边长为4的正方形ABCD中,P是BC边上一动点(不含B、C两点),将△ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将△CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA,NA.则以下结论中正确的有①②⑤(写出所有正确结论的序号)
如图,在边长为4的正方形ABCD中,P是BC边上一动点(不含B、C两点),将△ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将△CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA,NA.则以下结论中正确的有①②⑤(写出所有正确结论的序号)