题目内容
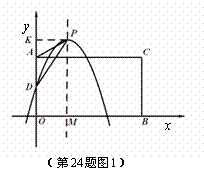
如图, 在平面直角坐标系中,点A,B分别是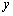 轴正半轴,
轴正半轴,  轴正半轴上两动点,
轴正半轴上两动点,  ,
, ,以AO,BO为邻边构造矩形AOBC,抛物线
,以AO,BO为邻边构造矩形AOBC,抛物线 交
交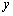 轴于点D,P为顶点,PM⊥
轴于点D,P为顶点,PM⊥ 轴于点M.
轴于点M.
(1)求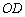 ,
, 的长(结果均用含
的长(结果均用含 的代数式表示).
的代数式表示).
(2)当 时,求该抛物线的表达式.
时,求该抛物线的表达式.
(3)在点 在整个运动过程中.
在整个运动过程中.
①若存在 是等腰三角形,请求出所有满足条件的
是等腰三角形,请求出所有满足条件的 的值.
的值.
 ②当点A关于直线DP的对称点
②当点A关于直线DP的对称点 恰好落在抛物线
恰好落在抛物线 的图象上时,请直接写出
的图象上时,请直接写出 的值.
的值.
解:(1)把x=0,代入 ,得
,得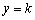 .∴
.∴ .
.
∵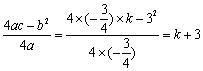 ,∴
,∴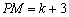 . (3分)
. (3分)
(2)∵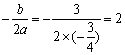 ,∴
,∴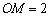 ,
,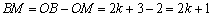 .
.
又∵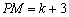 ,
, ,∴
,∴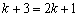 ,解得
,解得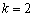 .
.
∴该抛物线的表达式为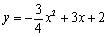 . (3分)
. (3分)
(3)①
Ⅰ)当点P在矩形AOBC外部时
如图1,过P作PK⊥OA于点K,当AD=AP时,
∵AD=AO-DO=2k-k=k,
∴AD=AP =k,KA=KO-AO=PM-AO=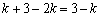
 KP=OM=2,在Rt△KAP中,
KP=OM=2,在Rt△KAP中,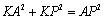
∴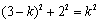 ,解得
,解得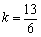 .
.
Ⅱ)当点P在矩形AOBC内部时
当PD=AP时,如图2,过P作PH⊥OA于H,
AD=k,HD=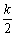 ,
,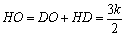
又∵HO=PM=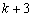 ,
,
∴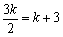 ,解得
,解得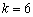 .
.
当DP=DA时,如图3,过D作PQ⊥PM于Q,
PQ=PM-QM=PM-OD=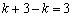
DQ=OM=2,DP=DA=k,
在Rt△DQP中,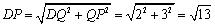 .
.
∴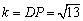 . (6分)
. (6分)
② .
.
 | |||
 | |||

练习册系列答案
相关题目

 ﹣
﹣
 =1的解为负数,则k的取值范围是 .
=1的解为负数,则k的取值范围是 .
 ;
;


 中的x和y都扩大3倍,分式的值( )
中的x和y都扩大3倍,分式的值( ) 3,0).
3,0).

 中,
中, ,垂足为
,垂足为 ,点
,点 在
在 上,
上, ,垂足为
,垂足为 .
. 与
与 平行吗?为什么?
平行吗?为什么? ,且
,且 ,求
,求 的度数.
的度数. 
