题目内容
 矩形OABC有两边在坐标轴的正半轴上,如图所示,双曲线y=
矩形OABC有两边在坐标轴的正半轴上,如图所示,双曲线y=| 6 |
| x |
| 2 |
| x |
考点:反比例函数综合题
专题:探究型
分析:先根据OA=3得出直线AB的解析式为x=3,把x=3代入反比例函数y=
即可求出D点坐标,由DG∥OA可得出直线DG的解析式,进而得出G点坐标,用待定系数法求出直线OE的解析式,进而可得出E点坐标,求出CE的长即可.
| 6 |
| x |
解答:解:∵矩形OABC中,OA=3,
∴直线AB的解析式为x=3,
∴
,
解得
,
∴D(3,2),
∵DG∥OA,
∴直线DG的解析式为y=2,
∴
,
解得
,
∴G(1,2),
设直线OE的解析式为y=kx(k≠0),把点G(1,2)代入得2=k,即直线OE的解析式为y=2x,
∴
,
解得
,
∴E(
,2
),
∴CE=
.
∴直线AB的解析式为x=3,
∴
|
解得
|
∴D(3,2),
∵DG∥OA,
∴直线DG的解析式为y=2,
∴
|
解得
|
∴G(1,2),
设直线OE的解析式为y=kx(k≠0),把点G(1,2)代入得2=k,即直线OE的解析式为y=2x,
∴
|
解得
|
∴E(
| 3 |
| 3 |
∴CE=
| 3 |
点评:本题考查的是反比例函数综合题,涉及到反比例函数与一次函数的交点问题、用待定系数法求一次函数的解析式等知识,难度适中.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
下列各式是分式的为( )
A、
| ||
B、
| ||
| C、x | ||
D、
|
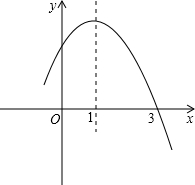 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,其中对称轴为:x=1,则下列4个结论中正确的结论有( )个
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,其中对称轴为:x=1,则下列4个结论中正确的结论有( )个①abc<0;②a+c>b;③2a+3b>0;④a+b>am2+bm(m≠1);⑤c<-2a.
| A、2个 | B、3个 | C、4个 | D、5个 |
三个等圆O1,O2,O3有公共点H,点A、B、C是其他交点,则H是三角形ABC的( )
| A、外心 | B、内心 | C、垂心 | D、重心 |
 一辆警车在高速公路的A处加满油,以每小时60千米的速度匀速行驶.已知警车一次加满油后,油箱内的余油量y(升)与行驶时间x(小时)的函数关系的图象如图所示的直线l上的一部分.如果警车要回到A处,且要求警车中的余油量不能少于10升,那么警车可以行驶到离A处的最远距离是
一辆警车在高速公路的A处加满油,以每小时60千米的速度匀速行驶.已知警车一次加满油后,油箱内的余油量y(升)与行驶时间x(小时)的函数关系的图象如图所示的直线l上的一部分.如果警车要回到A处,且要求警车中的余油量不能少于10升,那么警车可以行驶到离A处的最远距离是