题目内容
△ACB中AD、CE分别是BC、AB边上的高,连接DE,BC=nBE.(1)如图①当n=2时,
 =______.
=______.(2)如图②当n=
 时,求证:AC=
时,求证:AC= DE;
DE;(3)如图③当
 =
= 时,n=______
时,n=______
【答案】分析:三个小题的解法一致,都是通过两步相似来解答;首先根据已知条件,易证得△ABD∽△CBE,即可得:BD:BA=BE:BC,再加上公共角∠B,进而可证得△BDE∽△BAC,从而将DE:AC与BE:BC联系起来,由此得解.
解答:解:∵∠ADB=∠BEC=90°,∠B=∠B,
∴△BAD∽△BCE,
∴ ,∠B为公共角,
,∠B为公共角,
∴△BDE∽△BAC,
∴ ,即AC=nDE.
,即AC=nDE.
(1)当n=2时, =
= .
.
(2)(证法同上);
∵∠ADB=∠BEC=90°,∠B=∠B,
∴△BAD∽△BCE,∴ ,∠B为公共角,
,∠B为公共角,
∴△BDE∽△BAC,∴ ,∴AC=
,∴AC= DE.
DE.
(3)用上可知: ,故
,故 .
.
点评:此题主要考查的是相似三角形的判定和性质,难度不大.
解答:解:∵∠ADB=∠BEC=90°,∠B=∠B,
∴△BAD∽△BCE,
∴
 ,∠B为公共角,
,∠B为公共角,∴△BDE∽△BAC,
∴
 ,即AC=nDE.
,即AC=nDE.(1)当n=2时,
 =
= .
.(2)(证法同上);
∵∠ADB=∠BEC=90°,∠B=∠B,
∴△BAD∽△BCE,∴
 ,∠B为公共角,
,∠B为公共角,∴△BDE∽△BAC,∴
 ,∴AC=
,∴AC= DE.
DE.(3)用上可知:
 ,故
,故 .
.点评:此题主要考查的是相似三角形的判定和性质,难度不大.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目

 如图,在△ABC中,∠ABC=60゜,AD、CE分别平分∠BAC、∠ACB,AD、CE交于O.
如图,在△ABC中,∠ABC=60゜,AD、CE分别平分∠BAC、∠ACB,AD、CE交于O.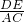 =______.
=______. 时,求证:AC=
时,求证:AC= 时,n=______.
时,n=______.
 =______.
=______. 时,求证:AC=
时,求证:AC= DE;
DE; =
= 时,n=______
时,n=______