题目内容
3.(1)2$\sqrt{12}$$+\sqrt{18}$$-\sqrt{27}$$-3\sqrt{32}$(2)2$\sqrt{\frac{1}{2}}$-6$\sqrt{\frac{1}{3}}$$+\sqrt{8}$
(3)($\sqrt{6}+\sqrt{5}$)2007×$(\sqrt{6}-\sqrt{5})$2006
(4)3($\sqrt{3}-π$)0-$\frac{\sqrt{20}-\sqrt{15}}{\sqrt{5}}$+(-1)2011.
分析 (1)先把各二次根式化为最简二次根式,然后合并即可;
(2)先把各二次根式化为最简二次根式,然后合并即可;
(3)先根据积的乘方得到原式=[($\sqrt{6}$+$\sqrt{5}$)($\sqrt{6}$+$\sqrt{5}$)]2006•($\sqrt{6}$+$\sqrt{5}$),然后利用平方差公式计算;
(4)先根据零指数幂和二次根式的除法法则运算,然后合并即可.
解答 解:(1)原式=4$\sqrt{3}$+3$\sqrt{2}$-3$\sqrt{3}$-12$\sqrt{2}$
=$\sqrt{3}$-9$\sqrt{2}$;
(2)原式=$\sqrt{2}$-2$\sqrt{3}$+2$\sqrt{2}$
=3$\sqrt{2}$-2$\sqrt{3}$;
(3)原式=[($\sqrt{6}$+$\sqrt{5}$)($\sqrt{6}$+$\sqrt{5}$)]2006•($\sqrt{6}$+$\sqrt{5}$)
=(6-5)]2006•($\sqrt{6}$+$\sqrt{5}$)
=$\sqrt{6}$+$\sqrt{5}$;
(4)原式=3×1-($\sqrt{20÷5}$-$\sqrt{15÷5}$)-1
=3-2+$\sqrt{3}$-1
=$\sqrt{3}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.也考查了零指数幂.

练习册系列答案
相关题目
14.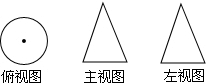 如图所示某几何体的三视图,则这个几何体是( )
如图所示某几何体的三视图,则这个几何体是( )
 如图所示某几何体的三视图,则这个几何体是( )
如图所示某几何体的三视图,则这个几何体是( )| A. | 三棱锥 | B. | 圆柱 | C. | 球 | D. | 圆锥 |
18.下列各式中,是最简二次根式的是( )
| A. | $\sqrt{0.3}$ | B. | $\sqrt{10}$ | C. | $\sqrt{20}$ | D. | $\sqrt{24}$ |
13.下列说法错误的是( )
| A. | 若△ABC中,a2=(b+c)(b-c),则△ABC是直角三角形 | |
| B. | 若△ABC中,a2+b2≠c2,则△ABC不是直角三角形 | |
| C. | 若△ABC中,a:b:c=13:5:12,则∠A=90° | |
| D. | 若△ABC中,a、b、c三边的长分别为n2-1、2n、n2+1(n>1),则△ABC是直角三角形 |
 如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+c过点A(-1,0)、B(3,0).C(2,3)三点,且与y轴交于点D.
如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+c过点A(-1,0)、B(3,0).C(2,3)三点,且与y轴交于点D.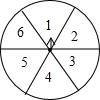 如图,是可以自由转动的转盘,该转盘被分成6个相等的扇形区域.
如图,是可以自由转动的转盘,该转盘被分成6个相等的扇形区域.