题目内容
13.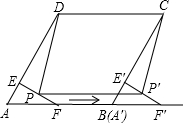 如图,在菱形ABCD中,∠A=60°,AD=8,F是AB的中点.过点F作FE⊥AD,垂足为E.将△AEF沿点A到点B的方向平移,得到△A'E'F'.设 P、P'分别是 EF、E'F'的中点,当点A'与点B重合时,四边形PP'CD的面积为( )
如图,在菱形ABCD中,∠A=60°,AD=8,F是AB的中点.过点F作FE⊥AD,垂足为E.将△AEF沿点A到点B的方向平移,得到△A'E'F'.设 P、P'分别是 EF、E'F'的中点,当点A'与点B重合时,四边形PP'CD的面积为( )| A. | 28$\sqrt{3}$ | B. | 24$\sqrt{3}$ | C. | 32$\sqrt{3}$ | D. | 32$\sqrt{3}$-8 |
分析 如图,连接BD,DF,DF交PP′于H.首先证明四边形PP′CD是平行四边形,再证明DF⊥PP′,求出DH即可解决问题.
解答 解:如图,连接BD,DF,DF交PP′于H.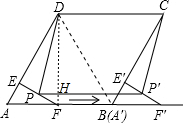
由题意PP′=AA′=AB=CD,PP′∥AA′∥CD,
∴四边形PP′CD是平行四边形,
∵四边形ABCD是菱形,∠A=60°,
∴△ABD是等边三角形,
∵AF=FB,
∴DF⊥AB,DF⊥PP′,
在Rt△AEF中,∵∠AEF=90°,∠A=60°,AF=4,
∴AE=2,EF=2$\sqrt{3}$,
∴PE=PF=$\sqrt{3}$,
在Rt△PHF中,∵∠FPH=30°,PF=$\sqrt{3}$,
∴HF=$\frac{1}{2}$PF=$\frac{\sqrt{3}}{2}$,
∵DF=4$\sqrt{3}$,
∴DH=4$\sqrt{3}$-$\frac{\sqrt{3}}{2}$=$\frac{7\sqrt{3}}{2}$,
∴平行四边形PP′CD的面积=$\frac{7\sqrt{3}}{2}$×8=28$\sqrt{3}$.
故选A.
点评 本题考查菱形的性质、平行四边形的判定和性质、等边三角形的判定和性质、解直角三角形等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考选择题中的压轴题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.一个不透明的盒子里有n个除颜色外其他完全相同的小球,其中有9个黄球.每次摸球前先将盒子里的球摇匀,任意摸出一个球记下颜色后再放回盒子,通过大量重复摸球实验后发现,摸到黄球的频率稳定在30%,那么估计盒子中小球的个数n为( )
| A. | 20 | B. | 24 | C. | 28 | D. | 30 |
3.在一个不透明的盒子里装着除颜色外完全相同的黑、白两种颜色的小球共40个,程程做摸球实验,她将盒子里面的小球搅匀后从中随机摸出一个小球,记下颜色后放回,不断重复上述过程,多次实验后,得到表中的数据,则盒子里的白球最可能有( )
| 摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
| 摸到白球的次数m | 62 | 122 | 179 | 302 | 481 | 599 | 1810 |
| A. | 30个 | B. | 28个 | C. | 24个 | D. | 16个 |
4.下列各式表示正确的是( )
| A. | $\sqrt{25}=±5$ | B. | $±\sqrt{25}=5$ | C. | $±\sqrt{{{(-5)}^2}}=-5$ | D. | $±\sqrt{25}=±5$ |
 阅读材料:
阅读材料: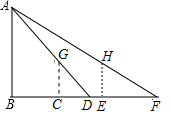 小强为测量一路灯杆AB的高度,在灯光下,小强在C处的影长为3米,沿BC方向行走了5米到E处,此时小强的影长为5米,若小强身高为1.7米,求路灯杆AB的高度.
小强为测量一路灯杆AB的高度,在灯光下,小强在C处的影长为3米,沿BC方向行走了5米到E处,此时小强的影长为5米,若小强身高为1.7米,求路灯杆AB的高度.