题目内容
13.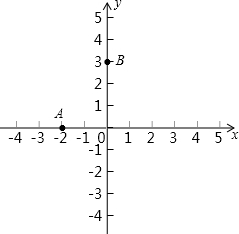 如图,平面直角坐标系中,点A在x轴上,点B在y轴上,OA=2,OB=3.
如图,平面直角坐标系中,点A在x轴上,点B在y轴上,OA=2,OB=3.(1)点A的坐标是(-2,0),点B的坐标是(0,3);(直接写答案)
(2)已知点P在y轴上,且△PAB的面积为5,请直接写出点P的坐标(0,-2)或(0,8);
(3)已知直线y=-3,请在图中画出此直线.若点C是直线y=-3上的一个点,且点C在第四象限内,联结BC与x轴相交于点D,试说明BD=CD的理由.
分析 (1)根据坐标的意义即可直接求得A和B的坐标;
(2)设P的坐标是(0,p),根据三角形的面积公式即可列出关于p的方程,从而求解;
(3)过点C做CE⊥x轴,垂足为E,然后证明△BOD和△CED即可证得.
解答 解:(1)A(-2,0),B(0,3);
(2)设P的坐标是(0,p),
则$\frac{1}{2}$×2×|p-3|=5,
解得:p=-2或8.
则P的坐标是P(0,-2)或(0,8);
(3)过点C做CE⊥x轴,垂足为E,
∵点C在直线y=-3上,
∴CE=3,
∵OB=3,
∴CE=OB(等量代换).
∵BO⊥x轴,CE⊥x轴,
∴∠BOD=∠CED=90°(垂直的意义).
∴在△BOD和△CED中,
$\left\{\begin{array}{l}∠BOD=∠CED(已证)\\∠BDO=∠CDE(对顶角相等)\\ BO=CE(已证)\end{array}\right.$
∴△BOD≌△CED,
∴BD=CD(全等三角形的对应边相等).
点评 本题是一次函数与全等三角形的判定与性质的综合应用,正确作出辅助线是本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.下列说法正确的是( )
| A. | 平移不改变图形的形状和大小,而旋转则改变图形的形状和大小 | |
| B. | 平移和旋转的共同点是改变了图形的位置,而图形的形状大小没有变化 | |
| C. | 图形可以向某方向平移一定距离,也可以向某方向旋转一定距离 | |
| D. | 在平移和旋转图形中,对应角相等,对应线段相等且平行 |
18.下列说法中,错误的是( )
| A. | (-4)2的平方根是-4 | B. | 5是25的算术平方根 | ||
| C. | -$\frac{1}{3}$是-$\frac{1}{27}$的立方根 | D. | -$\frac{5}{6}$是$\frac{25}{36}$的一个平方根 |
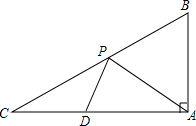 如图,在△ABC中,∠BAC=90°,∠C=30°,AB=$\sqrt{3}$,点D在AC边上,且CD=$\frac{1}{2}$,点P是斜边BC上的一个动点,求PA+PD的最小值.
如图,在△ABC中,∠BAC=90°,∠C=30°,AB=$\sqrt{3}$,点D在AC边上,且CD=$\frac{1}{2}$,点P是斜边BC上的一个动点,求PA+PD的最小值.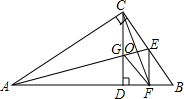 如图,在Rt△ABC中,∠ACB=90°,AE平分∠BAC,交BC于点E,CD⊥AB于点D,EF⊥AB于点F,CD交AE于点G,CF交AE于点O.求证:四边形CGFE是菱形.
如图,在Rt△ABC中,∠ACB=90°,AE平分∠BAC,交BC于点E,CD⊥AB于点D,EF⊥AB于点F,CD交AE于点G,CF交AE于点O.求证:四边形CGFE是菱形.