题目内容
已知AD是△ABC的高，CD=1，AD=BD=
，则∠BAC=________．
75°或15°
分析：高的位置分两种情形．根据三角函数的定义先求出∠BAD、∠CAD的度数，再相加或相减即可求出∠BAC的度数．
解答：
解：如图所示：
①tan∠BAD=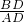
=1，∴∠BAD=45°，
tan∠CAD=
=
，∴∠BAD=30°，
∴∠BAC=45°+30°=75°；
②tan∠BAD=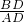=1，∴∠BAD=45°，
tan∠CAD==，∴∠BAD=30°，
∴∠BAC=45°-30°=15°．
故∠BAC=75°或15°．
点评：本题考查了三角函数的知识和分类讨论的思想．
分析：高的位置分两种情形．根据三角函数的定义先求出∠BAD、∠CAD的度数，再相加或相减即可求出∠BAC的度数．
解答：
解：如图所示：①tan∠BAD=
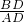=1，∴∠BAD=45°，tan∠CAD=
=，∴∠BAD=30°，∴∠BAC=45°+30°=75°；
②tan∠BAD=
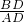=1，∴∠BAD=45°，tan∠CAD=
=，∴∠BAD=30°，∴∠BAC=45°-30°=15°．
故∠BAC=75°或15°．
点评：本题考查了三角函数的知识和分类讨论的思想．
练习册系列答案
相关题目
于点F，连接FB、FC．
3、如图，已知AD是△ABC的中线，AE=EF=FC，下面给出三个关系式：①AG：AD=1：2；②GE：BE=1：4；③GE：BE=3：4，其中正确的为（ ）
