题目内容
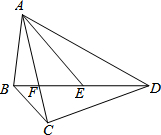 如图,四边形ABCD的对角线AC,BD交于点F,点E是BD上一点,且∠BAC=∠BDC=∠DAE.
如图,四边形ABCD的对角线AC,BD交于点F,点E是BD上一点,且∠BAC=∠BDC=∠DAE.(1)求证:△ABE∽△ACD;
(2)若BC=2,AD=6,DE=3,求AC的长.
考点:相似三角形的判定与性质
专题:
分析:(1)由∠BAC=∠DAE,易得∠BAE=∠CAD,又由∠BAC=∠BDC,∠BFA=∠CFD,可证得∠ABE=∠ACD,即可证得:△ABE∽△ACD.
(2)由△ABE∽△ACD,可得
=
,又由∠BAC=∠DAE,则可证得△ABC∽△AED,然后由相似三角形的对应边成比例,求得答案.
(2)由△ABE∽△ACD,可得
| AB |
| AC |
| AE |
| AD |
解答:解:(1)证法一:∵∠BAC=∠DAE,
∴∠BAC+∠CAE=∠DAE+∠CAE,
即∠BAE=∠CAD.
又∵∠BAC=∠BDC,∠BFA=∠CFD,
∴180°-∠BAC-∠BFA=180°-∠BDC-∠CFD,
即∠ABE=∠ACD.
∴△ABE∽△ACD.
证法二:∵∠BAC=∠DAE,
∴∠BAC+∠CAE=∠DAE+∠CAE,
即∠BAE=∠CAD.
又∵∠BEA=∠DAE+∠ADE,∠ADC=∠BDC+∠ADE,∠DAE=∠BDC,
∴∠AEB=∠ADC.
∴△ABE∽△ACD.
(2)∵△ABE∽△ACD,
∴
=
.
又∵∠BAC=∠DAE,
∴△ABC∽△AED,
∴
=
,
∴AC=
•AD=
×6=4.
∴∠BAC+∠CAE=∠DAE+∠CAE,
即∠BAE=∠CAD.
又∵∠BAC=∠BDC,∠BFA=∠CFD,
∴180°-∠BAC-∠BFA=180°-∠BDC-∠CFD,
即∠ABE=∠ACD.
∴△ABE∽△ACD.
证法二:∵∠BAC=∠DAE,
∴∠BAC+∠CAE=∠DAE+∠CAE,
即∠BAE=∠CAD.
又∵∠BEA=∠DAE+∠ADE,∠ADC=∠BDC+∠ADE,∠DAE=∠BDC,
∴∠AEB=∠ADC.
∴△ABE∽△ACD.
(2)∵△ABE∽△ACD,
∴
| AB |
| AC |
| AE |
| AD |
又∵∠BAC=∠DAE,
∴△ABC∽△AED,
∴
| BC |
| DE |
| AC |
| AD |
∴AC=
| BC |
| DE |
| 2 |
| 3 |
点评:此题考查了相似三角形的判定与性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
某种蛋白质分子的直径为251000埃,已知1埃=10-10米,则用科学记数法表示该蛋白质分子的直径是( )
| A、2.51×105米 |
| B、2.51×104米 |
| C、2.51×10-6米 |
| D、2.51×10-5米 |
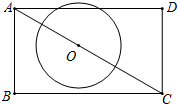 如图,已知矩形ABCD中,AB=2,BC=2
如图,已知矩形ABCD中,AB=2,BC=2