题目内容
 已知:平面直角坐标系xOy中,圆心在x轴上的⊙M与y轴交于点D(0,4)、点H,过H作⊙O的切线交x轴于点A,若点M(-3,0),则sin∠HAO的值为________.
已知:平面直角坐标系xOy中,圆心在x轴上的⊙M与y轴交于点D(0,4)、点H,过H作⊙O的切线交x轴于点A,若点M(-3,0),则sin∠HAO的值为________.

分析:连接MH,求出∠HAO=∠MHO,求出OD,OM,根据勾股定理求出MH,根据解直角三角形求出即可.
解答:
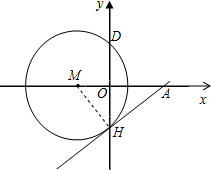 连接MH,
连接MH,∵D(0,4),M(-3,0),
∴OD=4,OM=3,
由垂径定理得:OH=OD=4,
在Rt△MHO中,由勾股定理得:MH=5,
∵AH为⊙M切线,
∴∠MHA=∠MOH=90°,
∴∠HAMO+∠AHO=90°,∠AHO+∠MHO=90°,
∴∠HAO=∠MHO,
∴sin∠HAO=sin∠MHO=
 =
= ,
,故答案为:
 .
.点评:本题考查了三角形的内角和定理,切线的性质,解直角三角形,垂径定理的应用,关键是求出MH的长和得出∠HAO=∠MHO.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
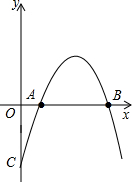 二次函数y=ax2+bx+c(a≠0)的图象经过点A、B,与y轴相交于点C.
二次函数y=ax2+bx+c(a≠0)的图象经过点A、B,与y轴相交于点C. (2013•浙江一模)如图,已知在平面直角坐标系中,点A(4,0)、B(-3,0),点C在y轴正半轴上,且tan∠CAO=1,点Q是线段AB上的动点,过点Q作QE∥AC交BC于点E.
(2013•浙江一模)如图,已知在平面直角坐标系中,点A(4,0)、B(-3,0),点C在y轴正半轴上,且tan∠CAO=1,点Q是线段AB上的动点,过点Q作QE∥AC交BC于点E.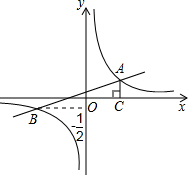 (2012•樊城区模拟)如图,已知在平面直角坐标系xOy中,一次函数y1=kx+b(k≠0)的图象与反比例函数y2=
(2012•樊城区模拟)如图,已知在平面直角坐标系xOy中,一次函数y1=kx+b(k≠0)的图象与反比例函数y2=