题目内容
如图，已知平行四边形ABCD边上一点F，BF：FC=4：1，AF交BD于E，求EF：AE的值．考点：平行四边形的性质,相似三角形的判定与性质
专题：
分析：首先根据已知条件设FC=k，则BC=5k；证明△BEF∽△DEA，列出比例式问题即可解决．
解答：解：∵BF：FC=4：1，
∴设FC=k，则BF=4k，BC=5k；
∵四边形ABCD为平行四边形，
∴AD=BC=5k；AD∥BC，
∴△BEF∽△DEA，
∴
=
=
=
，
即EF：AE的值为
．
解：∵BF：FC=4：1，∴设FC=k，则BF=4k，BC=5k；
∵四边形ABCD为平行四边形，
∴AD=BC=5k；AD∥BC，
∴△BEF∽△DEA，
∴
| EF |
| AE |
| BF |
| AD |
| 4k |
| 5k |
| 4 |
| 5 |
即EF：AE的值为
| 4 |
| 5 |
点评：该命题以平行四边形为载体，以考查平行四边形的性质、相似三角形的判定及其性质的应用为核心构造而成；解题的关键是灵活运用有关定理来分析、判断、推理或解答．
练习册系列答案
全能测控期末小状元系列答案
相关题目
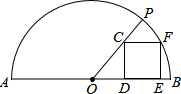如图所示，AB是半圆O的直径，且AB=20，正方形CDEF的四个顶点分别在半径OP，OB及