题目内容
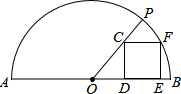 如图所示,AB是半圆O的直径,且AB=20,正方形CDEF的四个顶点分别在半径OP,OB及
如图所示,AB是半圆O的直径,且AB=20,正方形CDEF的四个顶点分别在半径OP,OB及 |
| BP |
考点:勾股定理,圆的认识
专题:
分析:连结OF,根据正方形的性质和等腰直角三角形的性质可得OD=CD=DE=EF,在Rt△OEF中,根据勾股定理可求EF的长,再根据正方形的面积公式可求正方形CDEF的面积.
解答: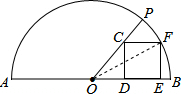 解:连结OF,
解:连结OF,
∵四边形CDEF是正方形,∠PCF=45°,
∴OD=CD=DE=EF,
∴OE=2EF,
∵AB是半圆O的直径,且AB=20,
∴OF=10,
在Rt△OEF中,EF2+OE2=OF2,
EF2+(2EF)2=102,
解得EF=2
,
故正方形CDEF的面积为:2
×2
=20.
 解:连结OF,
解:连结OF,∵四边形CDEF是正方形,∠PCF=45°,
∴OD=CD=DE=EF,
∴OE=2EF,
∵AB是半圆O的直径,且AB=20,
∴OF=10,
在Rt△OEF中,EF2+OE2=OF2,
EF2+(2EF)2=102,
解得EF=2
| 5 |
故正方形CDEF的面积为:2
| 5 |
| 5 |
点评:考查了勾股定理和圆的认识,关键是作出辅助线构造直角三角形.同时考查了正方形的性质和等腰直角三角形的性质,以及正方形的面积.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列数据中,哪一组不是勾股数( )
| A、7,24,25 |
| B、9,40,41 |
| C、3,4,5 |
| D、8,15,19 |
若|m|+|n|=0,则m,n( )
| A、相等 | B、异号 |
| C、互为相反数 | D、均为零 |
 如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4). 如图,已知平行四边形ABCD边上一点F,BF:FC=4:1,AF交BD于E,求EF:AE的值.
如图,已知平行四边形ABCD边上一点F,BF:FC=4:1,AF交BD于E,求EF:AE的值. 两个圆的半径和与半径差分别为a和b,则图中阴影部分的面积是多少?
两个圆的半径和与半径差分别为a和b,则图中阴影部分的面积是多少?