题目内容
 某研究小组计划测量篮球的直径,通过实验发现下面的测量方法:如图,将篮球放在水平的桌面上,在阳光的照射下,得到篮球的影子AB.设光线DA,CB分别与篮球相切于点E,F,则EF即为篮球的直径.若测得∠ABC=30°,AB的长为60cm,请计算出篮球的直径.
某研究小组计划测量篮球的直径,通过实验发现下面的测量方法:如图,将篮球放在水平的桌面上,在阳光的照射下,得到篮球的影子AB.设光线DA,CB分别与篮球相切于点E,F,则EF即为篮球的直径.若测得∠ABC=30°,AB的长为60cm,请计算出篮球的直径.考点:平行投影,切线的性质
专题:
分析:过点A作AO⊥AB,交EF于O,连结OB,直角三角形ABO中,有AB的长,可求∠ABO的度数,利用正切函数即可求出AO的长.
解答: 解:过点A作AO⊥AB,交EF于O,连结OB.
解:过点A作AO⊥AB,交EF于O,连结OB.
则OA=OE=OF,
在Rt△ABO中,AB=60cm,∠ABO=
∠ABC=15°,
∴AO=AB•tan∠AB0=60tan15°(cm).
∴球的直径为120tan15°cm.
 解:过点A作AO⊥AB,交EF于O,连结OB.
解:过点A作AO⊥AB,交EF于O,连结OB.则OA=OE=OF,
在Rt△ABO中,AB=60cm,∠ABO=
| 1 |
| 2 |
∴AO=AB•tan∠AB0=60tan15°(cm).
∴球的直径为120tan15°cm.
点评:此题考查了切线的性质以及三角函数的性质.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
相关题目
有下列图形:①线段;②角;③三角形;④等边三角形;⑤平行四边形.其中是中心对称图形的有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
 图中的四个小三角形都是等边三角形,边长为2cm,能通过平移△ABC得到其他三角形吗?若能,请画出平移的方向,并说出平移的距离.
图中的四个小三角形都是等边三角形,边长为2cm,能通过平移△ABC得到其他三角形吗?若能,请画出平移的方向,并说出平移的距离.
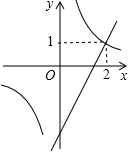 如图,已知反比例函数
如图,已知反比例函数