题目内容
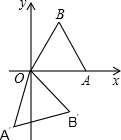如图，等边三角形OAB的顶点O在坐标原点，顶点A在x轴上，OA=2，将等边三角形OAB绕原点顺时针旋转105°至OA′B′的位置，则点B′的坐标为
- A.（
，-） - B.（-，）
- C.（-
，） - D.（，-）
A
分析：根据旋转的性质求出∠AOB′=45°，然后过点B′作B′C⊥x轴于C，判断出△OB′C是等腰直角三角形，根据等腰三角形直角边与斜边的关系求解即可．
解答：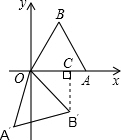
解：如图，∵△OAB是等边三角形，旋转角为105°，
∴∠AOB′=105°-60°=45°，
过点B′作B′C⊥x轴于C，
则△OB′C是等腰直角三角形，
∵OA=2，
∴OB′=2，
∴OC=B′C=2×
=，
∴点B′的坐标为（，-）．
故选A．
点评：本题考查了坐标与图形变化-旋转，是基础题，根据旋转角求出∠AOB′=45°然后作出等腰直角三角形是解题的关键．
分析：根据旋转的性质求出∠AOB′=45°，然后过点B′作B′C⊥x轴于C，判断出△OB′C是等腰直角三角形，根据等腰三角形直角边与斜边的关系求解即可．
解答：
解：如图，∵△OAB是等边三角形，旋转角为105°，∴∠AOB′=105°-60°=45°，
过点B′作B′C⊥x轴于C，
则△OB′C是等腰直角三角形，
∵OA=2，
∴OB′=2，
∴OC=B′C=2×
=，∴点B′的坐标为（
，-）．故选A．
点评：本题考查了坐标与图形变化-旋转，是基础题，根据旋转角求出∠AOB′=45°然后作出等腰直角三角形是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
（2013•临沂）如图，等边三角形OAB的一边OA在x轴上，双曲线
（2013•历城区一模）如图，等边三角形OAB的顶点O在坐标原点，顶点A在x轴上，OA=2，将等边三角形OAB绕原点顺时针旋转105°至OA′B′的位置，则点B′的坐标为（ ）
如图，等边三角形ABC内接于⊙O，连接OA，OB，OC，延长AO，分别交BC于点P，与⊙O交于点D，连接BD，CD．那么：①四边形BDCO是菱形，②若⊙O的半径为r，三角形的边长为
如图，等边三角形AOB绕点O旋转到△A′OB′的位置，且OA′⊥OB，则△AOB旋转了如图，等边三角形OAB的顶点O在坐标原点，顶点A在x轴上，OA=2，将等边三角形OAB绕原点顺时针旋转105°至OA′B′的位置，则点B′的坐标为（ ）
A．（ ， ） | B．（，） | C．（ ,  ） | D．（，） |