题目内容
如图,在四边 形ABCD中,∠A=∠BCD=90°,BC=CD,CE⊥AD,垂足为E.求证:AE=CE.
形ABCD中,∠A=∠BCD=90°,BC=CD,CE⊥AD,垂足为E.求证:AE=CE.
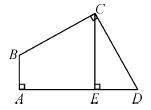
证明:作BF⊥CE于F.

∵∠BCF+∠DCE=90°,∠D+∠DCE=90°,
∴∠BCF=∠D.又BC=CD,
∴Rt△BCF≌Rt△CDE,
∴BF=CE.
又∠BFE=∠AEF=∠A=90°,
∴四边形ABFE是矩形,
∴BF=AE,
∴AE=CE.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案
相关题目

 只老鼠,猫头鹰至少要飞多少米(精确到0.1米)?
只老鼠,猫头鹰至少要飞多少米(精确到0.1米)?

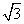 B.3
B.3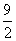
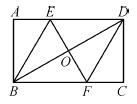



 cm,那么它的外接圆的半径的长度
cm,那么它的外接圆的半径的长度 为 cm.
为 cm.