题目内容
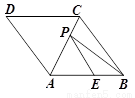
16. 如图,在平面直角坐标系xOy内有一点Q(3,4),那么射线OQ与x轴正半轴的夹角α的余弦值是$\frac{3}{5}$.
如图,在平面直角坐标系xOy内有一点Q(3,4),那么射线OQ与x轴正半轴的夹角α的余弦值是$\frac{3}{5}$.
分析 作QA⊥x轴于点A,在直角△OAQ中利用勾股定理求得OQ的长,然后根据余弦的定义求解.
解答  解:作QA⊥x轴于点A.
解:作QA⊥x轴于点A.
则OA=3,QA=4,
在直角△OAQ中,OQ=$\sqrt{O{A}^{2}+Q{A}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,
则cosα=$\frac{OA}{OQ}$=$\frac{3}{5}$.
故答案是:$\frac{3}{5}$.
点评 本题考查锐角三角函数的定义及运用:在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
4.已知等腰三角形中一个角等于100°,则这个等腰三角形的底角等于( )
| A. | 100° | B. | 40° | C. | 50° | D. | 100°或40° |
1.计算10ab3÷5ab的结果是( )
| A. | 2ab3 | B. | 2ab2 | C. | 2b3 | D. | 2b2 |
5. 如图,∠A是⊙O的圆周角,∠A=50°,则∠BOC的度数为( )
如图,∠A是⊙O的圆周角,∠A=50°,则∠BOC的度数为( )
 如图,∠A是⊙O的圆周角,∠A=50°,则∠BOC的度数为( )
如图,∠A是⊙O的圆周角,∠A=50°,则∠BOC的度数为( )| A. | 40° | B. | 50° | C. | 90° | D. | 100° |
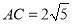 ,点E在边AB上,BE=2,点P是AC上的一个动点,则PB+PE的最小值为______.
,点E在边AB上,BE=2,点P是AC上的一个动点,则PB+PE的最小值为______.