Question

10．某数学兴趣小组对线段上的动点问题进行探究，已知AB=8．
问题思考：
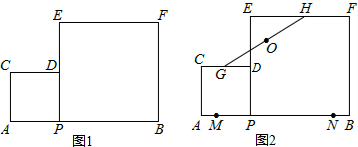
如图1，点P为线段AB上的一个动点，分别以AP、BP为边在同侧作正方形APDC、BPEF．
（1）分别连接AD、DF、AF，AF交DP于点K，当点P运动时，在△APK、△ADK、△DFK中，是否存在两个面积始终相等的三角形？请说明理由．
问题拓展：
（2）如图2，若点M、N是线段AB上的两点，且AM=BN=1，点G、H分别是边CD、EF的中点，请直接写出点P从M到N的运动过程中，GH的中点O所经过的路径的长及OM+ON的最小值．

Answer 1

分析 （1）如图1，只要证明AD∥PF，推出S_△ADP=S_△ADF，即S_△ADK+S_△AKP=S_△ADK+S_△DKF，由此即可解决问题．
（2）首先证明点O到AB的距离的定值，即点O的轨迹是平行于AB的线段．如图3中，当P与M重合时，作OT⊥BF于T，求出OT的长，如图4中，当点P与N重合时，作OT⊥PD于T，连接HT，延长HT交CD于K，求出OT的长即可解决点O 的运动路径的长；如图5中，作OT⊥BF于T，作点N关于OT的对称点R，连接MR与OT交于点O，此时OM+ON=OM+OR=RM（最短，理由是两点之间线段最短），在Rt△MNR理由勾股定理即可解决问题．

解答 解：（1）如图1，存在，△APK和△DFK的面积始终相等，连接PF．

∵四边形APDC，四边形WFBP都是正方形，
∴∠DAP=∠FPB=45°，
∴AD∥PF，
∴S_△ADP=S_△ADF，
∴S_△ADK+S_△AKP=S_△ADK+S_△DKF
∴S_△APK=S_△DFK，
∴当点P运动过程中，△APK和△DFK的面积始终相等；

（2）如图2中，过点O作RQ⊥AB于Q，交EF于P，延长CD交RQ于K，设正方形APDC的边长为a，正方形EFBP的边长为b．

在△OGK和△OHR中，
$\left\{\begin{array}{l}{∠GOK=∠HOR}\\{∠OKG=∠ORH=90°}\\{OG=OH}\end{array}\right.$，
∴△OGK≌△OHR，
∴OR=OK=$\frac{1}{2}$（b-a），
∴OQ=OK+KQ=Ok+AC=$\frac{1}{2}$（b-a）+a=$\frac{1}{2}$（a+b）=4，
∴点O到AB的距离的定值，即点O的轨迹是平行于AB的线段．
当P与M重合时，作OT⊥BF于T，则四边形EMQR是矩形，四边形OTFR是矩形，设ER=MQ=GK=a，

由（1）可知△OGK≌△OHR，
∴GK=RH，
∴$\frac{1}{2}$+a=$\frac{7}{2}$-a，
∴a=$\frac{3}{2}$，
∴OT=FR=7-$\frac{3}{2}$=$\frac{11}{2}$．
当点P与N重合时，作OT⊥PD于T，连接HT，延长HT交CD于K，

∵EF∥GD，GO=OH，
∴$\frac{GO}{OH}$=$\frac{DT}{TE}$=$\frac{KT}{TH}$=1，
∴TD=TE，TK=TH，
∵∠DTK=∠ETH，
∴△DTK≌△ETH，
∴DK=EH=$\frac{1}{2}$，GK=$\frac{7}{2}$-$\frac{1}{2}$=3，
∴OT=$\frac{1}{2}$GK=$\frac{3}{2}$，
综上所述点O运动的路径的长为$\frac{11}{2}$-$\frac{3}{2}$=4．

如图5中，作OT⊥BF于T，作点N关于OT的对称点R，连接MR与OT交于点O，此时OM+ON=OM+OR=RM（最短，理由是两点之间线段最短）

在Rt△MNR中，∵MN=8-1-1=6，RB=2BT=8，
∴RM=$\sqrt{M{N}^{2}+N{R}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10．
∴OM+ON的最小值为10．

点评 本题考查三角形综合题、正方形的性质、平行线的性质、轨迹问题、最短问题等知识，解题的关键是灵活运用所学知识解决问题，学会利用特殊点确定轨迹的长度问题，学会利用对称解决最短问题，属于中考压轴题．