题目内容
在△ 中,AD⊥BC,
中,AD⊥BC,

(1)利用尺规作图,作△
 外接圆⊙O;
外接圆⊙O;(2)判断:AC和⊙O的位置关系,并说明理由;
(3)若AC=10,AD=8,求⊙O的直径;
(1) -(2)AC是⊙O的切线,理由见解析(3)
-(2)AC是⊙O的切线,理由见解析(3) 解析:
解析:
解:(1) ------------2分
------------2分
(2)∵AD⊥BC
∴
∴
∵
∴
∴ ------------3分
------------3分
∵AB是圆O的直径
∴AC是⊙O的切线------------4分
(3)∵ ,AC=10,AD=8
,AC=10,AD=8
∴CD=6------------5分
∵

∴△ADC∽△BDA-----------6分
∴ -----------7分
-----------7分
∴
∴ ------------8分
------------8分
(1)先根据基本作图,作出线段AB的垂直平分线,交点就是圆心,再以AB的一半为半径画圆即可;
(2)AC是⊙O的切线,由于AD⊥BC,那么∠ADB=90°,即∠B+∠BAD=90°,而∠CAD=∠B,等量代换即可得∠CAD+∠BAD=90°,即∠BAC=90°,从而可证AC是⊙O的切线;
(3)由于∠CAD=∠B,∠ADC=∠BDA=90°,易证△ACD∽△BAD,在Rt△ACD中利用勾股定理可求CD,再利用比例线段可求AB
 -(2)AC是⊙O的切线,理由见解析(3)
-(2)AC是⊙O的切线,理由见解析(3) 解析:
解析:解:(1)
 ------------2分
------------2分(2)∵AD⊥BC
∴

∴

∵

∴

∴
 ------------3分
------------3分 ∵AB是圆O的直径
∴AC是⊙O的切线------------4分
(3)∵
 ,AC=10,AD=8
,AC=10,AD=8∴CD=6------------5分
∵


∴△ADC∽△BDA-----------6分
∴
 -----------7分
-----------7分∴

∴
 ------------8分
------------8分(1)先根据基本作图,作出线段AB的垂直平分线,交点就是圆心,再以AB的一半为半径画圆即可;
(2)AC是⊙O的切线,由于AD⊥BC,那么∠ADB=90°,即∠B+∠BAD=90°,而∠CAD=∠B,等量代换即可得∠CAD+∠BAD=90°,即∠BAC=90°,从而可证AC是⊙O的切线;
(3)由于∠CAD=∠B,∠ADC=∠BDA=90°,易证△ACD∽△BAD,在Rt△ACD中利用勾股定理可求CD,再利用比例线段可求AB

练习册系列答案
相关题目
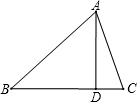 如图:在△ABC中,AD⊥BC,垂足是D.
如图:在△ABC中,AD⊥BC,垂足是D. 已知:如图,在△ABC中,AD⊥BC于D,BC=24,AD=18,矩形EFGH内接于△ABC,且EH=2EF,求矩形EFGH的周长.
已知:如图,在△ABC中,AD⊥BC于D,BC=24,AD=18,矩形EFGH内接于△ABC,且EH=2EF,求矩形EFGH的周长. 24、如图,在△ABC中,AD⊥BC,AD=12,BD=16,CD=5.
24、如图,在△ABC中,AD⊥BC,AD=12,BD=16,CD=5.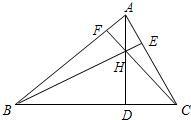 25、已知如图:在△ABC中,AD⊥BC于D,BE⊥AC于E,AD、BE相交于H,且BH=AC,连接CH并延长交AB于F,指出图中所有度数为45°的角,并任选一个来证明.
25、已知如图:在△ABC中,AD⊥BC于D,BE⊥AC于E,AD、BE相交于H,且BH=AC,连接CH并延长交AB于F,指出图中所有度数为45°的角,并任选一个来证明. 在△ABC中,AD⊥BC于点D,∠BAC=45°,BD=3,DC=2,求△ABC的面积.
在△ABC中,AD⊥BC于点D,∠BAC=45°,BD=3,DC=2,求△ABC的面积.