题目内容
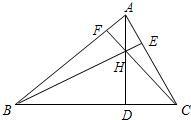25、已知如图：在△ABC中，AD⊥BC于D，BE⊥AC于E，AD、BE相交于H，且BH=AC，连接CH并延长交AB于F，指出图中所有度数为45°的角，并任选一个来证明．分析：根据已知可得∠HBD+∠BHD=∠AHE+∠HAE=90°，因为∠BHD=∠AHE，所以∠HBD=∠HAE，再利用AAS判定△BHD≌△ACD，得到DH=DC，根据等边对等角得到∠DHC=∠HCD=45°．
解答：证明：∵AD⊥BC于D，BE⊥AC于E
∴∠BDH=∠ADC=90°
∠HBD+∠BHD=∠AHE+∠HAE=90°
∵∠BHD=∠AHE
∴∠HBD=∠HAE
∵BH=AC
∴△BHD≌△ACD
∴DH=DC
∵∠HDC=90°
∴∠DHC=∠HCD=45°
∴∠BDH=∠ADC=90°
∠HBD+∠BHD=∠AHE+∠HAE=90°
∵∠BHD=∠AHE
∴∠HBD=∠HAE
∵BH=AC
∴△BHD≌△ACD
∴DH=DC
∵∠HDC=90°
∴∠DHC=∠HCD=45°
点评：此题主要考查了学生对全等三角形的判定及等腰三角形的判定的理解及运用．
练习册系列答案
相关题目
18、已知如图：在△ABC中，AB=AC，D在BC上，且DE∥AC交AB于E，点F在AC上，且DF=DC．求证：
（2012•通州区一模）已知如图，在△ABC中，AB=AC，∠ABC=α，将△ABC以点B为中心，沿逆时针方向旋转α度（0°＜α＜90°），得到△BDE，点B、A、E恰好在同一条直线上，连接CE．
已知如图，在△ABC中，∠B=30°，∠C=45°，AB-AC=2-
已知如图，在△ABC中，∠C=60°，AB=
已知如图，在△ABC中，AD平分∠BAC交BC于D，E为AD延长线上一点且∠ACE=∠B．求证：CD=CE．