题目内容
15.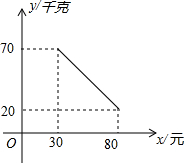 某商场销售一种商品,在一段时间内,该商品的销售量y(千克)与每千克的销售价x(元)满足一次函数关系(如图所示),其中30≤x≤80.
某商场销售一种商品,在一段时间内,该商品的销售量y(千克)与每千克的销售价x(元)满足一次函数关系(如图所示),其中30≤x≤80.(1)求y关于x的函数解析式;
(2)若该种商品每千克的成本为30元,当每千克的销售价为多少元时,获得的利润为600元?
分析 (1)设y与x之间的函数关系式为y=kx+b(k≠0),根据所给函数图象列出关于k、b的关系式,求出k、b的值即可;
(2)根据每天可获得600元的利润列出方程,解方程即可.
解答 解:(1)当30≤x≤80时,设y与x之间的函数关系式为y=kx+b(k≠0).
由所给函数图象可知,$\left\{\begin{array}{l}{30k+b=70}\\{80k+b=20}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-1}\\{b=100}\end{array}\right.$,
故y与x的函数关系式为y=-x+100;
(2)∵y=-x+100,依题意得
∴(x-30)(-x+100)=600,
x2-280x+18700=0,
解得x1=40,x2=90.
∵30≤x≤80,
∴取x=40.
答:当每千克的销售价为40元时,获得的利润为600元.
点评 本题考查了一元二次方程的应用、一次函数的应用、待定系数法确定一次函数的解析式;根据题意列出关于k、b的关系式和列出方程是解答此题的关键.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
 +(y+2)2=0,则yx=______.
+(y+2)2=0,则yx=______.
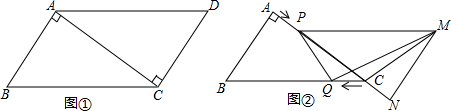
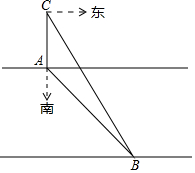 某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的北岸边点A处,测得河的南岸边点B在其南偏东45°方向,然后向北走20米到达C点,测得点B在点C的南偏东33°方向,求出这段河的宽度(结果精确到1米,参考数据sin33°≈0.54,cos33°≈0.84,tan33°≈0.65,$\sqrt{2}$≈1.41)
某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的北岸边点A处,测得河的南岸边点B在其南偏东45°方向,然后向北走20米到达C点,测得点B在点C的南偏东33°方向,求出这段河的宽度(结果精确到1米,参考数据sin33°≈0.54,cos33°≈0.84,tan33°≈0.65,$\sqrt{2}$≈1.41)