Question

【题目】在函数学习中，我们经历了“确定函数表达式一利用函数图象研究其性质一运用函数解决问题”的学习过程，在画函数图象时，我们通过描点或平移的方法画出了所学的函数图象，同时我们也学习了绝对值的意义|a|，结合上面经历的学习过程，现在来解决下面的问题：在函数y＝|kx﹣1|+b，当x＝1时，y＝﹣2；当x＝0时，y＝﹣1．

（1）求这个函数的表达式；

（2）请你结合以下表格在坐标系中画出该函数的图象．

（3）观察这个函效图象，请写出该函数的两条性质；

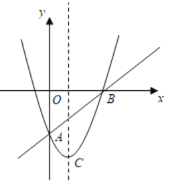
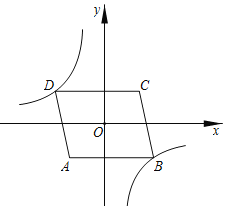
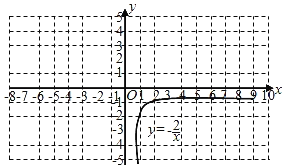
（4）已知函数y＝﹣（x＞0）的图象如图所示，请结合图象写出|kx﹣1|﹣﹣b（x0）的解集．

Answer 1

【答案】（1）；（2）见解析；（3）函数关于对称；函数有最小值-2；（4）

【解析】

（1）根据在函数y＝|kx﹣1|+b中，当x＝1时，y＝﹣2；当x＝0时，y＝﹣1，可以求得该函数的表达式；

（2）根据表格中的数据，描点、连线，可以画出该函数的图象；

（3）根据图象得出函数的性质即可；

（4）根据图象可以直接写出所求不等式的解集．

解：（1）∵在函数y＝|kx﹣1|+b中，当x＝1时，y＝﹣2；当x＝0时，y＝﹣1，

∴，得 ，

∴这个函数的表达式是y＝|x﹣1|﹣2；

（2）描点、连线，画出该函数的图象如图所示：

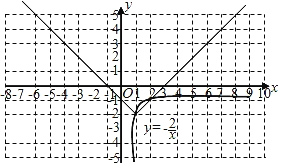
（3）观察这个函效图象，得出函数的性质：

①函数关于直线x＝1对称；

②函数有最小值﹣2；

（4）由函数图象可得，当1＜x＜2时，函数y＝（x＞0）的图像在函的上方，故的解集是1＜x＜2．