题目内容
已知△ABC和△A′B′C′中，
=
=
=
，且△ABC和△A′B′C′的周长之差是4，求△ABC和△A′B′C′的周长．
| AB |
| A′B′ |
| AC |
| A′C′ |
| BC |
| B′C′ |
| 6 |
| 5 |
考点：相似三角形的判定与性质
专题：
分析：先根据题意判断出△ABC∽△A′B′C′，再设△ABC的周长为x，则△A′B′C′的周长为x-4，再根据相似三角形的性质即可得出结论．
解答：解：∵△ABC和△A′B′C′中，
=
=
=
，
∴△ABC∽△A′B′C′．
∵△ABC和△A′B′C′的周长之差是4，
∴设△ABC的周长为x，则△A′B′C′的周长为x-4，
∴
=
，解得x=24，
∴24-4=20，
∴△ABC和△A′B′C′的周长分别是24，20．
| AB |
| A′B′ |
| AC |
| A′C′ |
| BC |
| B′C′ |
| 6 |
| 5 |
∴△ABC∽△A′B′C′．
∵△ABC和△A′B′C′的周长之差是4，
∴设△ABC的周长为x，则△A′B′C′的周长为x-4，
∴
| x |
| x-4 |
| 6 |
| 5 |
∴24-4=20，
∴△ABC和△A′B′C′的周长分别是24，20．
点评：本题考查的是相似三角形的判定与性质，熟知相似三角形周长的比等于相似比是解答此题的关键．
练习册系列答案
相关题目
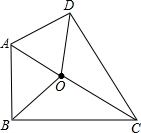已知，如图，在四边形ABCD中，OA、OB、OC、OD分别是∠A、∠B、∠C、∠D的平分线，求证：AB+CD=AD+BC．
如图，两条直线相交于一点组成的图形中有2对对顶角，三条直线相交于一点组成的图形中有6对对顶角，那么当1000条直线相交于一点所组成的图形中，可形成
△ABC中，∠C=90°，∠B=30°，AB的垂直平分线交BC于点D，垂足为E，BD=4cm，求AC，AB的长．