题目内容
 如图,AB∥CD,直线EF分别交AB,CD于E,F两点,∠BEF的平分线交CD于点G,若∠EFG=72°,则∠EGF等于
如图,AB∥CD,直线EF分别交AB,CD于E,F两点,∠BEF的平分线交CD于点G,若∠EFG=72°,则∠EGF等于
- A.36°
- B.54°
- C.72°
- D.108°
B
分析:根据平行线及角平分线的性质解答.
解答:∵AB∥CD,
∴∠BEF+∠EFG=180°,
∴∠BEF=180-72=108°;
∵EG平分∠BEF,
∴∠BEG=54°;
∵AB∥CD,
∴∠EGF=∠BEG=54°.
故选B.
点评:平行线有三个性质,其基本图形都是两条平行线被第三条直线所截,解答此类题关键是在复杂图形之中辨认出应用性质的基本图形,从而利用其性质和已知条件计算.
分析:根据平行线及角平分线的性质解答.
解答:∵AB∥CD,
∴∠BEF+∠EFG=180°,
∴∠BEF=180-72=108°;
∵EG平分∠BEF,
∴∠BEG=54°;
∵AB∥CD,
∴∠EGF=∠BEG=54°.
故选B.
点评:平行线有三个性质,其基本图形都是两条平行线被第三条直线所截,解答此类题关键是在复杂图形之中辨认出应用性质的基本图形,从而利用其性质和已知条件计算.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
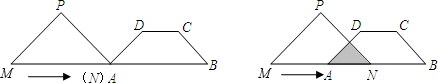
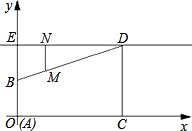 横坐标为x,纵坐标为y.
横坐标为x,纵坐标为y. 如图,将网格中的三条线段AB、CD、EF沿网格线(水平和铅直方向)平移,使它们首尾相接构成三角形,至少需要移动
如图,将网格中的三条线段AB、CD、EF沿网格线(水平和铅直方向)平移,使它们首尾相接构成三角形,至少需要移动
