题目内容
CD为⊙O的直径，弦AB⊥CD于M，若CM=12，DM=8，则AB等于
- A.4
- B.8
- C.8
- D.4
C
分析：根据题意画出图形，先由CM=12，DM=8求出⊙O的半径及OM的长，再由垂径定理得出AB=2AM，在Rt△AOM内利用勾股定理求出AM的长，进而可得出AB的长．
解答：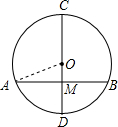
解：如图所示：
∵CM=12，DM=8，
∴OA=OD=
（CM+DM）=×20=10，
∴OM=OD-DM=10-8=2，
∵弦AB⊥CD于M，
∴AB=2AM，
在Rt△AOM中，
∵AM2=OA2-OM2，即AM2=102-22，解得AM=4，
∴AB=2AM=8．
故选C．
点评：本题考查的是垂径定理及勾股定理，根据题意作出辅助线，利用勾股定理求解是解答此题的关键．
分析：根据题意画出图形，先由CM=12，DM=8求出⊙O的半径及OM的长，再由垂径定理得出AB=2AM，在Rt△AOM内利用勾股定理求出AM的长，进而可得出AB的长．
解答：
解：如图所示：∵CM=12，DM=8，
∴OA=OD=
（CM+DM）=×20=10，∴OM=OD-DM=10-8=2，
∵弦AB⊥CD于M，
∴AB=2AM，
在Rt△AOM中，
∵AM2=OA2-OM2，即AM2=102-22，解得AM=4
，∴AB=2AM=8
．故选C．
点评：本题考查的是垂径定理及勾股定理，根据题意作出辅助线，利用勾股定理求解是解答此题的关键．
练习册系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
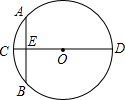如图，“圆材埋壁”是我国古代著名数学著作《九章算术》中的问题：“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何．”用几何语言可表述为：CD为⊙O的直径，弦AB⊥CD于E，CE=1寸，AB=10寸，则直径CD的长为（ ）
“圆材埋壁”是我国古代著名数学著作《九章算术》中的一个问题：“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何”此问题的实质就是解决下面的问题：“如图，CD为⊙O的直径，弦AB⊥CD于点E，CE=1，AB=10，求CD的长”．根据题意可得CD的长为
如图，已知CD为圆的直径，弦AB∥CD，连接BC、AC，若∠ABC=25°，则∠A的度数是