题目内容
 如图,是一个隧道的横截面,若它的形状是以O为圆心的圆的一部分,已知AB=12米,隧道最高处与地面距离(即CD)为8米,⊙O的半径OA为( )
如图,是一个隧道的横截面,若它的形状是以O为圆心的圆的一部分,已知AB=12米,隧道最高处与地面距离(即CD)为8米,⊙O的半径OA为( )分析:因为CD为高,根据垂径定理,CD平分AB,则AD=BD=6,在Rt△AOD中,有OA2=AD2+OD2,进而可求得半径OA.
解答:解:因为CD为高,
根据垂径定理:CD平分AB,
又路面AB宽为12米
则有:AD=
AB=6m,
设圆的半径是x米,
在Rt△AOD中,有OA2=AD2+OD2,
即:x2=62+(8-x)2,
解得:x=
,
所以圆的半径长是
米.
故选:C.
根据垂径定理:CD平分AB,
又路面AB宽为12米
则有:AD=
| 1 |
| 2 |
设圆的半径是x米,
在Rt△AOD中,有OA2=AD2+OD2,
即:x2=62+(8-x)2,
解得:x=
| 25 |
| 4 |
所以圆的半径长是
| 25 |
| 4 |
故选:C.
点评:此题主要考查了垂径定理的应用,解决与弦有关的问题时,往往需构造以半径、弦心距和弦长的一半为三边的直角三角形,若设圆的半径为r,弦长为a,这条弦的弦心距为d,则有等式r2=d2+(
)2成立,知道这三个量中的任意两个,就可以求出另外一个.
| a |
| 2 |

练习册系列答案
相关题目
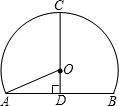 高速公路的隧道和桥梁最多.如图是一个隧道的横截面,若它的形状是以O为圆心的圆的一部分,路面AB=12米,净高CD=9米,则此圆的半径OA=( )
高速公路的隧道和桥梁最多.如图是一个隧道的横截面,若它的形状是以O为圆心的圆的一部分,路面AB=12米,净高CD=9米,则此圆的半径OA=( )A、
| ||
B、
| ||
C、
| ||
D、
|
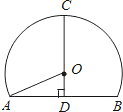 高速公路的隧道和桥梁最多.如图是一个隧道的横截面,若它的形状是以O为圆心的圆的一部分,路面AB=10米,净高CD=7米,则此圆的半径OA=( )
高速公路的隧道和桥梁最多.如图是一个隧道的横截面,若它的形状是以O为圆心的圆的一部分,路面AB=10米,净高CD=7米,则此圆的半径OA=( ) 高速公路的隧道和桥梁最多.如图是一个隧道的横截面,若它的形状是以O为圆心的圆的一部分,路面AB=10米,净高CD=7米,则此圆的半径OA=
高速公路的隧道和桥梁最多.如图是一个隧道的横截面,若它的形状是以O为圆心的圆的一部分,路面AB=10米,净高CD=7米,则此圆的半径OA= 如图,是一个隧道的横截面,若它的形状是以O为圆心的圆的一部分,已知AB=12米,隧道最高处与地面距离(即CD)为8米,⊙O的半径OA为
如图,是一个隧道的横截面,若它的形状是以O为圆心的圆的一部分,已知AB=12米,隧道最高处与地面距离(即CD)为8米,⊙O的半径OA为 米
米 米
米