题目内容
 高速公路的隧道和桥梁最多.如图是一个隧道的横截面,若它的形状是以O为圆心的圆的一部分,路面AB=10米,净高CD=7米,则此圆的半径OA=
高速公路的隧道和桥梁最多.如图是一个隧道的横截面,若它的形状是以O为圆心的圆的一部分,路面AB=10米,净高CD=7米,则此圆的半径OA=分析:根据垂径定理和勾股定理求解.
解答:解:设OA=r,则OD=7-r,AB=10.
由垂径定理可得AD=DB=
AB.
在直角三角形ADO中,OA2=OD2+AD2,
即r2=52+(7-r)2,
解得r=
≈5.29.
即此圆的半径OA=5.29米.
由垂径定理可得AD=DB=
| 1 |
| 2 |
在直角三角形ADO中,OA2=OD2+AD2,
即r2=52+(7-r)2,
解得r=
| 37 |
| 7 |
即此圆的半径OA=5.29米.
点评:相关链接:
垂径定理:垂直于弦的直径平分并且平分弦所在的弧.
勾股定理:在直角三角形中两条直角边的平方和等于斜边的平方.
垂径定理:垂直于弦的直径平分并且平分弦所在的弧.
勾股定理:在直角三角形中两条直角边的平方和等于斜边的平方.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
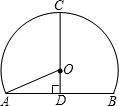 高速公路的隧道和桥梁最多.如图是一个隧道的横截面,若它的形状是以O为圆心的圆的一部分,路面AB=12米,净高CD=9米,则此圆的半径OA=( )
高速公路的隧道和桥梁最多.如图是一个隧道的横截面,若它的形状是以O为圆心的圆的一部分,路面AB=12米,净高CD=9米,则此圆的半径OA=( )A、
| ||
B、
| ||
C、
| ||
D、
|
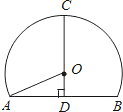 高速公路的隧道和桥梁最多.如图是一个隧道的横截面,若它的形状是以O为圆心的圆的一部分,路面AB=10米,净高CD=7米,则此圆的半径OA=( )
高速公路的隧道和桥梁最多.如图是一个隧道的横截面,若它的形状是以O为圆心的圆的一部分,路面AB=10米,净高CD=7米,则此圆的半径OA=( )
 =10米,净高
=10米,净高 =7米,则此圆的半径
=7米,则此圆的半径 =( )
=( ) D.
D.