题目内容
2.已知abc≠0,且a+b+c=0.设x=$\frac{|a+b|}{c}+\frac{|b+c|}{a}+\frac{|a+c|}{b}$,求3x2-5x-7的值.分析 根据a+b+c=0,得到a+b=-c,b+c=-a,a+c=-b,根据绝对值的性质化简,即可解答.
解答 解:∵abc≠0,且a+b+c=0,
∴a+b=-c,b+c=-a,a+c=-b,
∴x=$\frac{|a+b|}{c}+\frac{|b+c|}{a}+\frac{|a+c|}{b}$=$\frac{|-c|}{c}+\frac{|-a|}{a}+\frac{|-b|}{b}$,
∵a,b,c可能为2正1负或1正2负,
∴x=1或-1,
当x=1时,3x2-5x-7=3-5-7=-9,
当x=-1时,3x2-5x-7=3+5-7=1.
点评 本题考查了代数式求值,解决本题的关键是确定a,b,c的正负.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
7.已知α,β是一元二次方程x2-5x-2=0的两个不相等的实数根,则α+β+αβ的值为( )
| A. | -1 | B. | 9 | C. | 3 | D. | 27 |
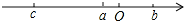 有理数a、b,c在数轴上的对应点如图,且a、b,c满足条件:|a|=1,|b|=2,|c|=5.
有理数a、b,c在数轴上的对应点如图,且a、b,c满足条件:|a|=1,|b|=2,|c|=5. 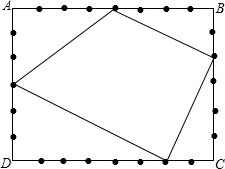 如图,矩形ABCD中,AB=8,AD=6,四边上各取一个整点(即到边的端点距离为正整数的点),并且由这4个点为顶点的四边形的面积为25,那么这样的4个点共有7种不同的取法.
如图,矩形ABCD中,AB=8,AD=6,四边上各取一个整点(即到边的端点距离为正整数的点),并且由这4个点为顶点的四边形的面积为25,那么这样的4个点共有7种不同的取法.