��Ŀ����
��ͼ����ƽ��ֱ������ϵ�У�������y=��x2+ax+b��x����A��1��0����B��3��0�����㣬��P�����������ڵ�һ�����ڵ�һ�㣬ֱ��BP��y���ཻ�ڵ�C��
��1����������y=��x2+ax+b�Ľ���ʽ��
��2������P���߶�BC���е�ʱ�����P�����ꣻ
��3���ڣ�2���������£���sin��OCB��ֵ��

���𰸡�(1) y=��x2+4x��3��(2) ��P������Ϊ�� ��
�� ����(3)
����(3)  .
.
����������������1������A��B����������y=-x 2+ax+b�����a��b�ɵý���ʽ��
��2����C�������Ϊ0�ɵ�P������꣬��P���������루1���������߽���ʽ����P�����ꣻ
��3����P�������ɵ�C�����꣬A��B��C�����꣬���ù��ɶ����ɵ�BC��������sin��OCB= �ɵý����
�ɵý����
�������
��1������A��B����������y=��x2+ax+b�ɵã�
 ��
��
��ã�a=4��b=��3��
�������ߵĽ���ʽΪ��y=��x2+4x��3��
��2���ߵ�C��y���ϣ�
����C�������x=0��
�ߵ�P���߶�BC���е㣬
���P������xP= =
= ��
��
�ߵ�P��������y=��x2+4x��3�ϣ�
��yP=
 ��3=
��3= ��
��
���P�������� ��
�� ����
����
��3���ߵ�P������Ϊ�� ��
�� ������P���߶�BC���е㣬
������P���߶�BC���е㣬
���C��������Ϊ2�� ��0=
��0= ��
��
���C��������0�� ����
����
��BC= =
= ��
��
��sin��OCB= =
= =
= ��
��
�㾦��������Ҫ�����˴���ϵ��������κ�������ʽ�����κ���ͼ�������ʣ���ֱ�������Σ����ɶ����������е���õ�P�������ǽ�����Ĺؼ���
�����͡������
��������
24
��ͼ����O�ǡ�ABC�����Բ��BC�ǡ�O��ֱ������ABC=30�㣬����B����O������BD����CA���ӳ��߽��ڵ�D����뾶AO���ӳ��߽��ڵ�E������A����O������AF����ֱ��BC���ӳ��߽��ڵ�F��
��1����֤����ACF�ס�DAE��
��2����S��AOC= ����DE�ij���
����DE�ij���
��3������EF����֤��EF�ǡ�O�����ߣ�

 ��������ܸ�ϰϵ�д�
��������ܸ�ϰϵ�д�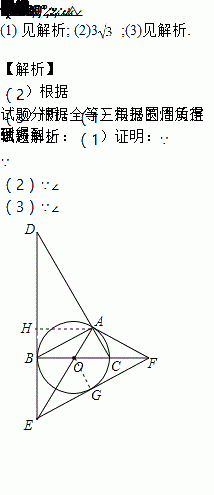


 ��ֵΪ0����x��ֵΪ ( )
��ֵΪ0����x��ֵΪ ( )

 �����ѽ⼯�������ϱ�ʾ����.
�����ѽ⼯�������ϱ�ʾ����. B.
B.  C.
C.  D.
D. 