题目内容
解不等式（2x+1）（3x-2）＞0时，根据有理数乘法法则“两数相乘，同号得正”有
①，或
②，解不等式①，得x＞
；解不等式②，得x＜
，则不等式（2x+1）（3x-2）＞0的解集为x＞或x＜，请参照例题，解不等式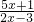
＜0．
解：根据题意得①
，或②
，
解不等式①，得-
＜x＜
；解不等式②无解，
所以原不等式的解集为-＜x＜．
分析：根据题中的解题方法可把原不等式化为①，或②，然后分别解两个不等式组，再得到原不等式的解集．
点评：本题考查了解一元一次不等式组：求解出两个不等式的解集，然后按照“同大取大，同小取小，大于小的小于大的取中间，小于小的大于大的无解”确定不等式组的解集．
，或②，解不等式①，得-
＜x＜；解不等式②无解，所以原不等式的解集为-
＜x＜．分析：根据题中的解题方法可把原不等式化为①
，或②，然后分别解两个不等式组，再得到原不等式的解集．点评：本题考查了解一元一次不等式组：求解出两个不等式的解集，然后按照“同大取大，同小取小，大于小的小于大的取中间，小于小的大于大的无解”确定不等式组的解集．
练习册系列答案
步步高达标卷系列答案
相关题目