Question

【题目】如图，在菱形ABCD中，AB=5，对角线AC=6，若过点A作AE⊥BC，垂足为E，则sinB的值为（　　）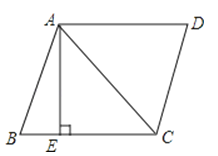

A.
B.
C.
D.

Answer 1

【答案】C
【解析】解：连接BD，交AC于O点，
∵四边形ABCD是菱形，
∴AB=BC=CD=AD=5，
∴AC⊥BD，AO=AC，BD=2BO，
∴∠AOB=90°，
∵AC=6，
∴AO=3，
∴B0==4，
∴DB=8，
∴菱形ABCD的面积是×ACDB=×6×8=24，
∴BCAE=24，
AE= ，
所以sinB= ，
故选C．

连接BD，根据菱形的性质可得AC⊥BD，AO=AC，然后根据勾股定理计算出BO长，再算出菱形的面积，然后再根据面积公式BCAE=ACBD可得答案．
【考点精析】利用菱形的性质对题目进行判断即可得到答案，需要熟知菱形的四条边都相等；菱形的对角线互相垂直，并且每一条对角线平分一组对角；菱形被两条对角线分成四个全等的直角三角形；菱形的面积等于两条对角线长的积的一半．