Question

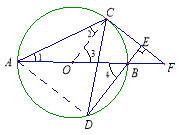
【题目】如图，AB为⊙O直径，C、D为⊙O上不同于A、B的两点，∠ABD=2∠BAC，连接CD.过点C作CE⊥DB，垂足为E，直线AB与CE相交于F点.

（1）求证：CF为⊙O的切线；

（2）当BF=5,时，求BD的长.

Answer 1

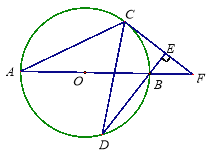
【答案】（1）证明见解析；（2）9.

【解析】

试题分析：（1）连接，证明即可证明CF为⊙O的切线.

（2）连接，由∽得到，在Rt△BEF和Rt△ABD中应用锐角三角函数定义即可求得BD的长.

试题解析：（1）如图，连接.

∵, ∴

又∵∴

又∵，∴ ∴OC∥DB.

∵CE⊥DB，∴.

又∵为⊙的半径，∴为⊙O的切线.

（2）如图，连接.

在Rt△BEF中，∠BEF=90°, BF=5, ，∴.

∵OC∥BE, ∴∽.∴

设⊙的半径为r, ∴ ∴.

∵AB为⊙O直径，∴.∴.

∵, ∴.

∴ ∴∴．