题目内容
已知菱形的周长为20cm,两个邻角的比是1:2,这个菱形较短的对角线的长 .
考点:菱形的性质
专题:
分析:依题意,根据菱形的性质首先求出边长,然后推出对角线与菱形的两边构成的三角形为等边三角形,最后可解答.
解答:解:已知菱形的周长为20cm,则菱形的边长是20×
=5(cm);
两个邻角的比是1:2,则较大的角是120°,较小的角是60°,这个菱形较短的对角线所对的角是60°;
根据菱形的性质得到,较短的对角线与菱形的两边构成的三角形是等边三角形,
所以,菱形较短的对角线的长等于菱形的边长5cm.
故答案为:5cm.
| 1 |
| 4 |
两个邻角的比是1:2,则较大的角是120°,较小的角是60°,这个菱形较短的对角线所对的角是60°;
根据菱形的性质得到,较短的对角线与菱形的两边构成的三角形是等边三角形,
所以,菱形较短的对角线的长等于菱形的边长5cm.
故答案为:5cm.
点评:此题主要考查了菱形的性质以及等边三角形的判定等知识,根据等边三角形的性质求解是解题关键.

练习册系列答案
相关题目
下列从左到右的变形,其中是因式分解的是( )
| A、(x+1)2=x2+2x+1 |
| B、x2-10x+25=(x-5)2 |
| C、(x+7)(x-7)=x2-49 |
| D、x2-2x+2=(x-1)2+1 |
若(x-5)(x+2)=x2+px+q,则p、q的值是( )
| A、3,10 |
| B、-3,-10 |
| C、-3,10 |
| D、3,-10 |
在实数-
, 0,
,π,
,其中无理数的个数为( )
| 2 |
| 3 |
| 9 |
| 3 | 4 |
| A、1 | B、2 | C、3 | D、4 |
 如图,折叠长方形的一边AD,点D落在BC边的点F处,已知:AB=8cm,BC=10cm,则△EFC的周长=
如图,折叠长方形的一边AD,点D落在BC边的点F处,已知:AB=8cm,BC=10cm,则△EFC的周长=
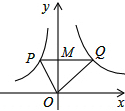 如图,若点M是y轴正半轴上任意一点,过点M作PQ∥x轴,分别交函数y=
如图,若点M是y轴正半轴上任意一点,过点M作PQ∥x轴,分别交函数y=