Question

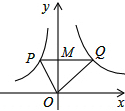如图，若点M是y轴正半轴上任意一点，过点M作PQ∥x轴，分别交函数y=

k1

x

（x＜0）和y=

k2

x

（x＞0）的图象于点P和Q，连接OP和OQ．以下列结论：
①∠POQ不可能等于90°；
②

PM

QM

=

k1

k2

； 
③这两个函数的图象一定关于y轴对称；  
④若S_△POM=S_△QOM，则k₁+k₂=0；
⑤△POQ的面积是

1

2

（|k₁|+|k₂|）．
其中正确的有

 

（填写序号）．

Answer 1

考点：反比例函数综合题,反比例函数系数k的几何意义

专题：推理填空题

分析：根据∠POQ的变化规律可以断定①错误；根据

PM

QM

为正，而

k1

k2

为负可以断定②错误
；根据两个反比例函数的图象关于y轴对称时比例系数是互为相反数可以断定③错误；
根据反比例函数比例系数的几何意义可以断定④和⑤正确．

解答：解：①点M接近点O时，∠POQ接近180°，点M沿着y轴正方向运动的过程中，∠POQ越来越小，越来越接近于0°，从接近180°到接近0°的过程中，必然存在∠POQ等于90°的情况，所以①错误．
②由图可知：k₁＜0，k₂＞0，则

k1

k2

＜0，而

PM

QM

＞0，所以②错误．
③反比例函数y=

k1

x

（x＜0）图象关于y轴对称的图象的解析式为y=-

k1

x

（x＞0），仅当k₂=-k₁时，这两个函数的图象才关于y轴对称，所以③错误．
④因为PQ∥x轴，x轴⊥y轴，所以PQ⊥y轴．所以S_△POM=

1

2

.

k1

.

=-

1

2

k₁，S_△QOM=

1

2

.

k2

.

=

1

2

k₂．若S_△POM=S_△QOM，则-

1

2

k₁=

1

2

k₂，即k₁+k₂=0，所以④正确．
⑤由④得：S_△POM=

1

2

.

k1

.

，S_△QOM=

1

2

.

k2

.

．所以S_△POQ=

1

2

（|k₁|+|k₂|）．所以⑤正确．
故答案为：④、⑤．

点评：本题主要考查了反比例函数比例系数的几何意义，以及反比例函数图象与其比例系数符号的关系；本题还注重推理能力的考查，是一道好题．