题目内容
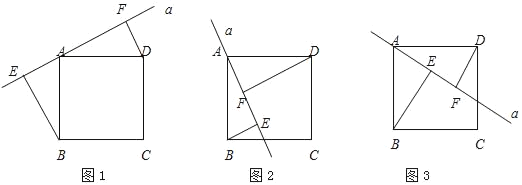
【题目】如图,点E是矩形ABCD的边CD上一点,把△ADE沿AE对折,点D的对称点F恰好落在BC上,已知折痕AE=![]() cm,且tan∠EFC=
cm,且tan∠EFC=![]() ,那么该矩形的周长为________.
,那么该矩形的周长为________.

【答案】72cm
【解析】在矩形ABCD中,AB=CD,AD=BC,∠B=∠D=90°,
∵△ADE沿AE对折,点D的对称点F恰好落在BC上,
∴∠AFE=∠D=90°,AD=AF,
∵∠EFC+∠AFB=180°-90°=90°,
∠BAF+∠AFB=90°,
∴∠BAF=∠EFC,
∵tan∠EFC=![]() ,
,
∴设BF=3x、AB=4x,
在Rt△ABF中,AF=![]() =5x,
=5x,
∴AD=BC=5x,
∴CF=BC-BF=5x-3x=2x,
∵tan∠EFC=![]() ,
,
∴CE=CFtan∠EFC=2x![]() =
=![]() x,
x,
∴DE=CD-CE=4x-![]() x=
x=![]() x,
x,
在Rt△ADE中,AD2+DE2=AE2,
即(5x)2+(![]() x)2=(10
x)2=(10![]() )2,
)2,
整理得,x2=16,
解得x=4,
∴AB=4×4=16cm,AD=5×4=20cm,
矩形的周长=2×(16+20)=72cm,
故答案为:72cm.

练习册系列答案
相关题目