题目内容
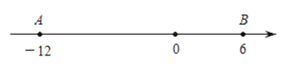
【题目】如图，数轴上
两点开始时所对应的数分别是
和6.两点各自以一定的速度在数轴上运动，且
点的运动速度为2个单位长度∕秒.
（1）若点
为两点初始时线段
的中点，则点所表示的数是_____；
（2）两点同时出发相向而行，在原点处相遇，求
点的运动速度；
（3）若两点按（2）中的速度同时出发，向数轴正方向运动，几秒时两点相距6个单位长度？
【答案】（1）
；（2）
点的运动速度为1个单位长度/秒；（3）当
两点运动12秒或24秒时相距6个单位长度.
【解析】
（1）先求出数轴上两点开始时，AB的值，6减去AB的一半，即可求解；
（2）设点的运动速度为
个单位长度/秒，根据等量关系，列出方程，即可求解；
（3）设两点运动
秒时相距6个单位长度，分两种情况讨论：①当点
在点的左侧时，②当点在点的右侧时，分别求解，即可．
（1）∵数轴上两点开始时所对应的数分别是
和6，
∴AB=6-(-12)=18，
∵点
为两点初始时线段
的中点，
∴点所表示的数是：6-9=，
故答案是：．
（2）设点的运动速度为个单位长度/秒，
由题意得：
，解得：
．
答：点的运动速度为1个单位长度/秒．
（3）设两点运动秒时相距6个单位长度，由题意得：
①当点在点的左侧时，
，
解得：
；
②当点在点的右侧时，
，
解得：
．
答：当两点运动12秒或24秒时相距6个单位长度．
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
