题目内容
【题目】如图，在平面直角坐标系中，点
为原点，
为等边三角形，
，
分别为
， 
边上的动点，点，点同时从点
出发，若以
个单位每秒的速度从点向点运动，点以2个单位每秒的速度从点向点
运动，设运动时间为
．
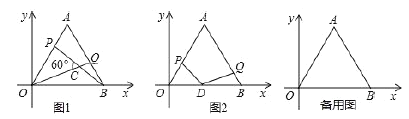
(1)如图1，已知点的坐标为
，且满足
，求点坐标:
(2)如图1．连接
，
交于点
，请问当为何值时，
；
(3)如图2，
为
边上的中点，，在运动过程中，，，三点是否能构成使
的等腰三角形，若能，试求:①运动时间；②此时四边形
的面积:若不能．请说明理由．
【答案】（1）
；（2）当
时，
；（3）能，①
；②
【解析】
（1）根据题意可得a、b的值，即可求出点A的坐标；
（2）根据等边三角形的性质可得AO=BO=AB=6，
，从而可证得
，可得OP=AQ，即可求t的值；
（3）过点
作
，
，连接
，通过证明
，
，可得OF=BE，DF=DE，PF=EQ，可得AP+AQ=2AF，可求t的值，根据三角形面积公式可求四边形APDQ的面积．
解：（1）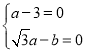
解得：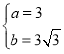
∴
，
故答案为：；
（2）∵
是等边三角形，点
∴
∵
∴
∴
，且
，
∴（
）
∴
∴
∴
∴当时
，
故答案为：；
（3）如图，过点作，，连接
∵
是等边三角形，是
中点，点
∴
，
，
又∵
∴（
）
∴
，
∵
∴
∴
∵，
∴（
）
∴
∵
，
，
∴
∴
，
∴
∵
∴
∴
∴当时,，
，
是所构成
的等腰三角形
∵
∴
∴
，
故答案为：能，①；②．
练习册系列答案
相关题目
